题目内容
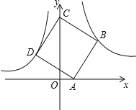
【题目】已知:如图,点![]() 在双曲线
在双曲线![]() (其中
(其中![]() )上,点
)上,点![]() 在双曲线
在双曲线![]() (其中
(其中![]() )上,点
)上,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴的正半轴上,且点
轴的正半轴上,且点![]() 、
、![]() 、
、![]() 、
、![]() 围成的四边形为正方形.
围成的四边形为正方形.
![]() 求
求![]() 的值;
的值;
![]() 设点
设点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的值.
的值.
【答案】(1)k=9;(2)a=1.
【解析】
(1)把B的坐标代入求出即可;
(2)过D作DE⊥x于点E,过点B作BF⊥x于点F,证△DAE≌△ABF,推出DE=AF=3﹣a,AE=FB=3,OE=3﹣a,从而求得D的坐标(a﹣3,3﹣a),代入y=![]() 即可求得a的值.
即可求得a的值.
(1)∵点B(3,3)在双曲线y=![]() (其中x>0)上,∴3=
(其中x>0)上,∴3=![]() ,∴k=3×3=9;
,∴k=3×3=9;
(2)过D作DE⊥x于点E,过点B作BF⊥x于点F,则∠DEA=∠AF B=90°.
∵点B(3,3),∴BF=3,OF=3.
∵A的坐标为(a,0),∴OA=a,AF=3﹣a.
∵四边形ABCD是正方形,∴AD=AB,∠DAB=90°,∴∠DAE+∠BAF=90°.
又∵∠DAE+∠ADE=90°,∴∠ADE=∠BAF.
在△DAE和△ABF中,∵ ,∴△DAE≌△ABF(AAS),∴DE=AF=3﹣a,AE=FB=3,∴OE=3﹣a.
,∴△DAE≌△ABF(AAS),∴DE=AF=3﹣a,AE=FB=3,∴OE=3﹣a.
又∵点D在第二象限,∴D(a﹣3,3﹣a).
∵点D在双曲线y=![]() (其中x<0)上,∴3﹣a=
(其中x<0)上,∴3﹣a=![]() ,∴a=1或a=5(不合题意,舍去),∴a=1.
,∴a=1或a=5(不合题意,舍去),∴a=1.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目