题目内容
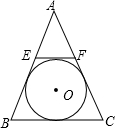如图△ABC中，AB=AC，EF∥BC，且⊙O内切于四边形BCFE．（1）当
| AE |
| BE |
| 1 |
| 2 |
（2）当
| AE |
| BE |
| 1 |
| n |
分析：作辅助线，利用圆的切线的性质构造直角三角形，求出相应各边之间的长度比，即可求出三角函数值．
解答：解：连接AO并延长交EF于点D，交BC于点H，则AH⊥BC，连接OG，则OG⊥AB
（1）∵∠BAH+∠AOG=90°，∠B+∠BAH=90°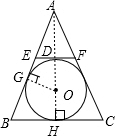
∴∠AOG=∠B，
∵EF∥BC
∴
=
=
设⊙O的半径为r，则
=
∵AD=
=r
∴AO=2r
又∵OG=r
∴AG=
=
r
∴sinB=
；
（2）sinB=
．
设AB与⊙O相切于点G，连接OG，则OG⊥AB
∴∠AOG=∠B
∵EF∥BC
∴
=
=
设⊙O的半径为r，则
=
∵AD=
∴AO=AD+r=
r
又∵OG=r
∴AG=
=
=
r
∴sinB=sin∠AOG=
=
=
．
（1）∵∠BAH+∠AOG=90°，∠B+∠BAH=90°
∴∠AOG=∠B，
∵EF∥BC
∴
| AD |
| DH |
| AE |
| EB |
| 1 |
| 2 |
设⊙O的半径为r，则
| AD |
| 2r |
| 1 |
| 2 |
∵AD=
| 2r |
| 2 |
∴AO=2r
又∵OG=r
∴AG=
| (2r)2-r2 |
| 3 |
∴sinB=
| ||
| 2 |
（2）sinB=
2
| ||
| n+2 |
设AB与⊙O相切于点G，连接OG，则OG⊥AB
∴∠AOG=∠B
∵EF∥BC
∴
| AD |
| DH |
| AE |
| EB |
| 1 |
| n |
设⊙O的半径为r，则
| AD |
| 2r |
| 1 |
| n |
∵AD=
| 2r |
| n |
∴AO=AD+r=
| n+2 |
| n |
又∵OG=r
∴AG=
| AO2-OG2 |
(
|
2
| ||
| n |
∴sinB=sin∠AOG=
| AG |
| AO |
| ||||
|
2
| ||
| n+2 |
点评：解题时要仔细分析（1），虽然（1）较简单，但是可以为（2）提供思路：求出各边的比，再求三角函数值．
练习册系列答案
华东师大版一课一练系列答案
孟建平名校考卷系列答案
相关题目
13、如图△ABC中，AB=AC，BD平分∠ABC，且△ABC∽△BDC，则∠A=
8、如图△ABC中，AB=3，AC=2，BO平分∠ABC，CO平分∠ACB．DE过点O交AB于D，交AC于E，且DE∥BC．则△ADE周长为
如图△ABC中，AB=AC，M是BC中点，D，E分别在AB，AC上，且BD=CE，求证：ME=MD．
已知：如图△ABC中，AB=AC，AD和BE是高，它们交于点H，且AE=BE，
如图△ABC中，AB=6，AC=