Question

【题目】计算：
（1）解方程组：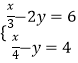
（2）求不等式﹣2＜ ≤2的整数解．

Answer 1

【答案】
（1）解： ，①﹣②×2得，﹣x=﹣12，解得x=12，

把x=12代入①得，4﹣2y=6，解得y=﹣1，

故方程组的解为：

（2）解：原不等式化为不等式组 ，

解①得，x＞﹣ ，解②得，x≤ ，

所以不等式组的解集为，﹣ ＜x≤ ．

所以，原不等式的整数解是﹣4，﹣3，﹣2，﹣1，0，1

【解析】（1）先用加减消元法求出x的值，再用代入消元法求出y的值即可；（2）把不等式化为不等式组的形式，分别求出各不等式的解集，再求出其公共解集即可．
【考点精析】本题主要考查了解二元一次方程组和一元一次不等式组的整数解的相关知识点，需要掌握二元一次方程组：①代入消元法；②加减消元法；使不等式组中的每个不等式都成立的未知数的值叫不等式组的解，一个不等式组的所有的解组成的集合，叫这个不等式组的解集(简称不等式组的解)才能正确解答此题．