Question

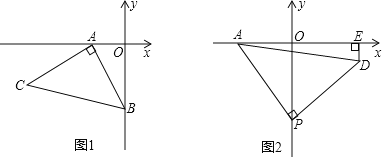
【题目】如图1，OA＝1，OB＝3，以A为直角顶点，AB为腰在第三象限作等腰Rt△ABC．

（1）求点C的坐标;

（2）如图2，P为y轴负半轴上的一个动点，当点P向下运动时，以P点为直角顶点，PA为腰作等腰Rt△APD，过D作DE⊥x轴于E点，求PO-DE的值．

Answer 1

【答案】见解析

【解析】分析】（1）如图1，过C作CD⊥x轴于D．构建全等三角形：△CDA≌△AOB（AAS），则AD=OB=3，CD=OA=1，故OD=4，所以易求C（﹣4，﹣1）；

（2）如图2，过点Q作QR⊥y轴于R．则四边形QEOR是矩形，通过证△OPA≌△RQP（AAS），推知OA=PR，则OR=OP﹣PR=OP﹣OA，所以OP﹣OR=OA=1，即OP﹣QE=1，始终保持不变．

试题解析：解：（1）如图，过C作CD⊥x轴于D．

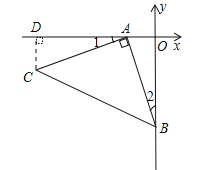
∵∠BAC=90°，∠AOB=90°，∴∠1+∠OAB=∠2+∠OAB=90°，∴∠1=∠2．

在△CDA与△AOB中，∵∠CDA=∠AOB，∠1=∠2，CA=AB，∴△CDA≌△AOB（AAS），

∴AD=OB=3，CD=OA=1，∴OD=4，∴C（﹣4，﹣1）；

（2）如图，过点Q作QR⊥y轴于R．

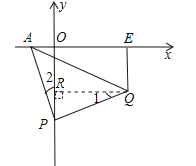
则四边形QEOR是矩形，∴QE=OR．

∵∠APQ=90°，∴∠1+∠QPR=∠2+∠QPR=90°，∴∠1=∠2．

在△APO与△PQR中，∵∠AOP=∠PRQ，∠1=∠2，AP=PQ，∴△OPA≌△RQP（AAS），∴OA=PR，∴OR=OP﹣PR=OP﹣OA，∴OP﹣OR=OA=1，即OP﹣QE=1，始终保持不变．