题目内容
【题目】如图,△OAB中,OA=OB=10cm,∠AOB=80°,以点O为圆心,半径为6cm的优弧弧MN分别交OA,OB于点M,N.
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得OP′.求证:AP=BP′;
(2)点T在左半弧上,若AT与弧相切,求AT的长.

【答案】(1)见解析;(2)8
【解析】试题分析:(1)首先根据已知得出∠AOP=∠BOP′,进而得出△AOP≌△BOP′,即可得出答案;(2)利用切线的性质得出∠ATO=90°,再利用勾股定理求出AT的长.
(1)证明:∵∠AOB=∠POP′=80°,
∴∠AOB+∠BOP=∠POP′+∠BOP,
即∠AOP=∠BOP′
在△AOP与△BOP′中
OA=OB,
∠AOP=∠BOP,
OP=OP′,
∴△AOP≌△BOP′,
∴AP=BP′.
(2)∵AT与弧相切,连结OT.

∴OT⊥AT,
在Rt△AOT中,根据勾股定理得,AT=![]() ,
,
∵OA=10,OT=6
∴AT=8.

练习册系列答案
相关题目
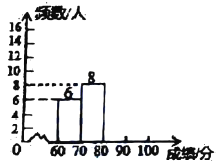
【题目】某大学举行了百科知识竞赛,为了解此次竞赛成绩的情况,随机抽取部分参赛学生的成绩,整理并制作出如下不完整的统计表和统计图,请根据图表信息解答以下问题:

组别 | 成绩 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
(1)表中![]() ___________.
___________.
(2)补全频数分布直方图
(3)计算扇形统计图中“![]() ”对应的圆心角度数.
”对应的圆心角度数.
(4)该大学共有![]() 人参加竞赛,若成绩在
人参加竞赛,若成绩在![]() 分以上(包括
分以上(包括![]() 分)的为“优”等,根据抽样结果,估计该校参赛学生成绩达到“优”等的人数.
分)的为“优”等,根据抽样结果,估计该校参赛学生成绩达到“优”等的人数.