Question

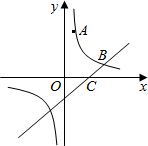
如图，已知反比例函数的图象经过点A，B，点A的坐标为（1，3），点B的纵坐标为1，点C的坐标为（2，0）
（1）求该反比例函数的解析式；
（2）求直线BC的解析式；
（3）当x为何值时，一次函数的函数值大于反比例函数的值．

Answer 1

分析：（1）把点A的坐标代入反比例函数的解析式，即可求解；
（2）根据（1）中的解析式求得点B的坐标，再进一步运用待定系数法求得一次函数的解析式；
（3）先求出反比例函数与一次函数的交点，然后观察直线落在双曲线上方的部分对应的x的值即为所求．

解答：解：（1）设所求反比例函数的解析式为y=

k

x

（k≠0）．
∵点A（1，3）在此反比例函数的图象上，
∴3=

k

1

，
∴k=3．
故所求反比例函数的解析式为y=

3

x

；

（2）设直线BC的解析式为y=nx+b（n≠0）．
∵点B在反比例函数y=

3

x

的图象上，点B的纵坐标为1，设B（m，1），
∴1=

3

m

，m=3．
∴点B的坐标为（3，1）．
由题意，得

3n+b=1 2n+b=0

解得

n=1 b=-2

．
∴直线BC的解析式为y=x-2；

（3）解方程组

y= 3 x y=x-2

，得

x=3 y=1

或

x=-1 y=-3

，
∴当-1＜x＜0或x＞3时，一次函数的值大于反比例函数的值．

点评：本题考查用待定系数法确定反比例函数的解析式以及根据函数图象解不等式的知识点，难易程度适中．