题目内容
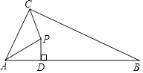
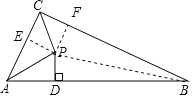
【题目】如图,在△ABC中,∠ACB=90°,∠ACB与∠CAB的平分线交于点P,PD⊥AB于点D,若△APC与△APD的周长差为![]() ,四边形BCPD的周长为12+
,四边形BCPD的周长为12+![]() ,则BC等于______.
,则BC等于______.
【答案】6
【解析】
过P作PE⊥AC于E,PF⊥BC于F,连接PB,根据已知条件得到PB平分∠ABC,推出矩形CEPF是正方形,设CE=x,得到CF=PE=x,PC![]() x,根据角平分线的性质得到PE=PD,根据全等三角形的性质得到AD=AE,同理BD=BF,根据已知条件即可得到结论.
x,根据角平分线的性质得到PE=PD,根据全等三角形的性质得到AD=AE,同理BD=BF,根据已知条件即可得到结论.
过P作PE⊥AC于E,PF⊥BC于F,连接PB.
∵∠ACB与∠CAB的平分线交于点P,∴PB平分∠ABC.
∵∠ACB=90°,∴四边形CEPF是矩形.
∵CP是∠ACB的角平分线,∴PF=PE,∴矩形CEPF是正方形,∴设CE=x,∴CF=PE=x,PC![]() x.
x.
∵AP是∠CAB的角平分线,∴PE=PD.
∵AP=AP,∴Rt△PAE≌Rt△PAD(HL),∴AD=AE,同理BD=BF.
∵△APC与△APD的周长差为![]() ,∴PC
,∴PC![]() ,∴CE=CF=PD=1.
,∴CE=CF=PD=1.
∵四边形BCPD的周长为12![]() ,∴2BF+PC+PD+CF=12
,∴2BF+PC+PD+CF=12![]() ,∴BF
,∴BF![]() 5,∴BC=6.
5,∴BC=6.
故答案为:6.

练习册系列答案
相关题目