Question

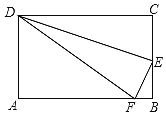
【题目】如图，点B在线段AC上，点D，E在AC的同侧，∠A＝∠C＝90°，BD⊥BE，AD＝BC.

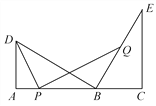
(1)求证：AC＝AD＋CE；

(2)若AD＝3，AB＝5，点P为线段AB上的动点，连接DP，作PQ⊥DP，交直线BE于点Q，当点P与A，B两点不重合时，求的值．

Answer 1

【答案】（1）详见解析；（2）.

【解析】试题分析：（1）根据同角的余角相等求出∠1=∠E，再利用“角角边”证明△ABD和△CEB全等，根据全等三角形对应边相等可得AB=CE，然后根据AC=AB+BC整理即可得证；

（2）过点Q作QF⊥BC于F，根据△BFQ和△BCE相似可得，然后求出QF=BF，再根据△ADP和△FPQ相似可得，然后整理得到（AP-BF）（5-AP）=0，从而求出AP=BF，最后利用相似三角形对应边成比例可得，从而得解．

试题解析：（1）∵BD⊥BE，

∴∠1+∠2=180°-90°=90°，

∵∠C=90°，

∴∠2+∠E=180°-90°=90°，

∴∠1=∠E，

∵在△ABD和△CEB中，

，

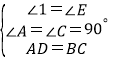∴△ABD≌△CEB（AAS），

∴AB=CE，

∴AC=AB+BC=AD+CE；

（2）如图，过点Q作QF⊥BC于F，

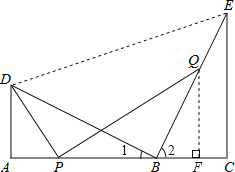
则△BFQ∽△BCE，

∴，

即 ，

∴QF=BF，

∵DP⊥PQ，

∴∠APD+∠FPQ=180°-90°=90°，

∵∠APD+∠ADP=180°-90°=90°，

∴∠ADP=∠FPQ，

又∵∠A=∠PFQ=90°，

∴△ADP∽△FPQ，

∴，

即，

∴5AP-AP2+APBF=3BF，

整理得，（AP-BF）（AP-5）=0，

∵点P与A，B两点不重合，

∴AP≠5，

∴AP=BF，

由△ADP∽△FPQ得，，

∴．