题目内容
【题目】为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子水平放置在离B(树底)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,求树AB的高度. 
【答案】解:过点E作EF⊥BD于点E,则∠1=∠2, ∵∠DEF=∠BEF=90°,
∴∠DEC=∠AEB,
∵CD⊥BD,AB⊥BD,
∴∠CDE=∠ABE=90°,
∴△CDE∽△ABE,
∴ ![]() =
= ![]() ,
,
∵DE=3.2米,CD=1.6米,EB=8.4米,
∴ ![]() =
= ![]() ,
,
解得AB=4.2(米).
答:树AB的高度为4.2米.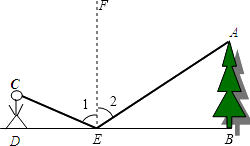
【解析】先过E作EF⊥BD于点E,再根据入射角等于反射角可知,∠1=∠2,故可得出∠DEC=∠AEB,由CD⊥BD,AB⊥BD可知∠CDE=∠ABE,进而可得出△CDE∽△ABE,再由相似三角形的对应边成比例即可求出大树AB的高度.
【考点精析】通过灵活运用相似三角形的应用,掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解即可以解答此题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目