Question

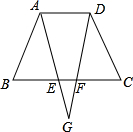
已知：如图，点E、F、G、H分别是梯形ABCD四条边上的中点，AD∥BC，AB=CD=EG=4．
（1）求梯形ABCD的周长；
（2）∠1与∠2是否相等？为什么？
（3）求证：四边形EFGH是菱形．

Answer 1

（1）由已知，得：EG是梯形的中位线，
∴AD+BC=2×4=8，
∴梯形ABCD的周长=AD+BC+CD+AD，
=4+4+8=16；

（2）∠1=∠2
由已知得：EB=GC=

1

2

AB，BF=CF=

1

2

BC，
而AB=CD，∴∠B=∠C，
∴△EBF≌△GCF
∴∠1=∠2；

（3）证法一：连接AC、BD，
在梯形ABCD中，AB=CD，∴AC=BD
在△ABD中，∵点E、H分别为AB、AD的中点，
∴EH=

1

2

BD，
同理：FG=

1

2

BD，EF=

1

2

AC，GH=

1

2

AC，
∴EF=FG=GH=HE=

1

2

BD，
∴四边形EFGH是菱形．