题目内容
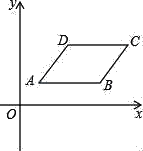
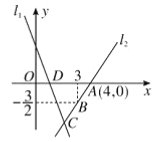
【题目】如图，在矩形OABC中，A（1，0），C（0，2），双曲线y=
（0＜k＜2）的图象分别交AB，CB于点E，F，连接OE，OF，EF，S△OEF=2S△BEF，则k值为_____．
【答案】
【解析】
设E点坐标为（1，m），则F点坐标为（
，2），根据三角形面积公式得到S△BEF=
（1-）（2-m），根据反比例函数k的几何意义得到S△OFC=S△OAE=m，由于S△OEF=S矩形ABCO-S△OCF-S△OEA-S△BEF，列方程即可得到结论．
解：∵四边形OABC是矩形，BA⊥OA，A（1，0），
∴设E点坐标为（1，m），则F点坐标为（ ，2），
则S△BEF=（1-）（2-m），S△OFC=S△OAE=m，
∴S△OEF=S矩形ABCO-S△OCF-S△OEA-S△BEF=2-m-m-（1-）（2-m），
∵S△OEF=2S△BEF，
∴2-m-m-（1-）（2-m）=2（1-）（2-m），
整理得
（m-2）2+m-2=0，解得m1=2（舍去），m2=，
∴E点坐标为（1，）；
∴k=，
故答案为：.
练习册系列答案
相关题目
