题目内容
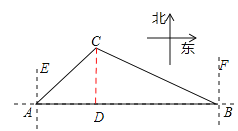
【题目】如图,一艘海轮在A点时测得灯塔C在它的北偏东42°方向上,它沿正东方向航行80海里后到达B处,此时灯塔C在它的北偏西55°方向上.
(1)求海轮在航行过程中与灯塔C的最短距离(结果精确到0.1);
(2)求海轮在B处时与灯塔C的距离(结果保留整数).
(参考数据:sin55°≈0.819,cos55°≈0.574,tan55°≈1.428,tan42°≈0.900,tan35°≈0.700,tan48°≈1.111)

【答案】(1)海轮在航行过程中与灯塔C的最短距离是34.4海里;
(2)海轮在B处时与灯塔C的距离约为60海里.
【解析】试题分析:(1)过点C作CD⊥AB于点D,则CD的长为海轮在航行过程中与灯塔C的最短距离.
(2)在Rt△BCD中,根据55°角的余弦值即可求出海轮在B处时与灯塔C的距离.
试题解析:解:(1)如答图,过点C作CD⊥AB于点D,
依题意得:∠ACD=∠CAE=42°,∠BCD=∠CBF=55°,
设CD的长为x海里,
在Rt△ACD中,tan42°=![]() ,则AD=xtan42°,
,则AD=xtan42°,
在Rt△BCD中,tan55°=![]() ,则BD=xtan55°,
,则BD=xtan55°,
∵AB=80,∴AD+BD="80." ∴xtan42°+xtan55°=80,解得:x≈34.4.
答:海轮在航行过程中与灯塔C的最短距离是34.4海里.
(2)在Rt△BCD中,cos55°=![]() ,∴BC=
,∴BC=![]() ≈60海里.
≈60海里.
答:海轮在B处时与灯塔C的距离是60海里.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目