题目内容
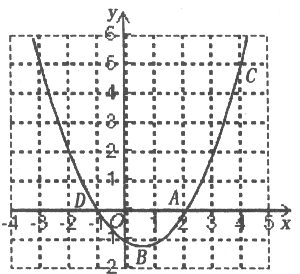
【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点。
(1)求二次函数的表达式;
(2)设二次函数的图象与x轴的另一个交点为D,求出点D的坐标;
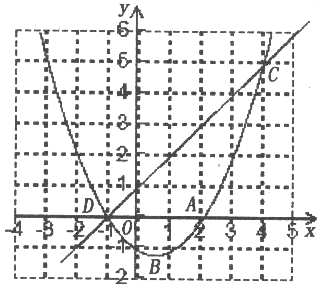
(3)在同一坐标系中画出直线y=x+1,根据图象直接写出当x在什么范围内时,一次函数的值大于二次函数的值。
【答案】(1)、y=![]() x2-
x2-![]() x-1;(2)、(-1,0);(3)、图像见解析;-1<x<4
x-1;(2)、(-1,0);(3)、图像见解析;-1<x<4
【解析】
试题分析:(1)、利用待定系数法求出函数解析式;(2)、求出当y=0时x的值,从而得出点D的坐标;(3)、根据图像的画法画出一次函数图像,然后得出x的取值范围.
试题解析:(1)、∵二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点,
 , ∴a=
, ∴a=![]() ,b=
,b=![]() ,c=-1, ∴二次函数的解析式为y=
,c=-1, ∴二次函数的解析式为y=![]() x2-
x2-![]() x-1;
x-1;
(2)、当y=0时,得![]() x2-
x2-![]() x-1=0; 解得x1=2,x2=-1, ∴点D坐标为(-1,0);
x-1=0; 解得x1=2,x2=-1, ∴点D坐标为(-1,0);
(3)、图象如图,当一次函数的值大于二次函数的值时, x的取值范围是-1<x<4。

练习册系列答案
相关题目