题目内容
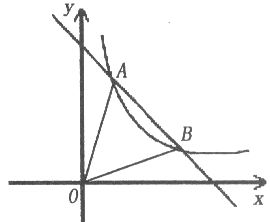
【题目】如图,一次函数y=k1x+b的图象与反比例函数y=![]() 的图象交于A(1,4),B(3,m)两点。
的图象交于A(1,4),B(3,m)两点。
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积。
【答案】(1)、y=![]() ;y=-
;y=-![]() x+
x+![]() ;(2)、
;(2)、![]()
【解析】
试题分析:(1)、根据点A的坐标得出反比例函数解析式,根据反比例函数解析式得出点B的坐标,然后利用待定系数法求出一次函数的解析式;(2)、设直线与x轴的交点为C,然后利用△AOC的面积减去△BOC的面积得出答案.
试题解析:(1)、∵点A(1,4)在y=![]() 的图象上, ∴k2=l×4=4,∴反比例函数为y=
的图象上, ∴k2=l×4=4,∴反比例函数为y=![]() ,
,
又∵B(3,m)在y=![]() 的图象上, ∴3m=4,解得m=
的图象上, ∴3m=4,解得m=![]() ,∴B(3,
,∴B(3,![]() ),
),
∵A(1,4)和B(3,![]() )都在直线y=k1x+b上, ∴
)都在直线y=k1x+b上, ∴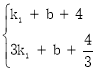 ,解得
,解得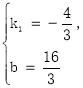 ,
,
∴一次函数解析式为y=-![]() x+
x+![]() ;
;
(2)、设直线y=-![]() x+
x+![]() 与x轴交于点C, 当y=0时,-
与x轴交于点C, 当y=0时,-![]() x+
x+![]() =0, 解得x=4,则C(4,0),
=0, 解得x=4,则C(4,0),
∴S△AOB=S△ACO-S△BOC=![]() ×4×4-
×4×4-![]() ×4×
×4×![]() =
=![]() 。
。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目