题目内容
 如图,已知⊙O1与⊙O2的半径分别为r1,r2,⊙O2经过⊙O1的圆心O1,且两圆相交于A,B两点,C为⊙O2上的点,连接AC交⊙O1于D点,再连接BC,BD,AO1,AO2,O1O2,有如下四个结论:①∠BDC=∠AO1O2;②
如图,已知⊙O1与⊙O2的半径分别为r1,r2,⊙O2经过⊙O1的圆心O1,且两圆相交于A,B两点,C为⊙O2上的点,连接AC交⊙O1于D点,再连接BC,BD,AO1,AO2,O1O2,有如下四个结论:①∠BDC=∠AO1O2;②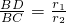 ;③AD=DC; ④BC=DC.其中正确结论的序号为________.
;③AD=DC; ④BC=DC.其中正确结论的序号为________.
①②④
分析:①延长O2O1交圆O1于M,连接AB、AM、BM、O2B,根据相交两圆的性质推出O2O1是AB的垂直平分线,得出∠AO1O2= ∠AO1B=∠AMB,根据圆内接四边形的性质得出∠AMB=∠BDC,即可判断;②证△BDC∽△AO1O2即可;③无法证出BD=DC,即可判断③;④由△BDC∽△AO1O2,得出∠O2AO1=∠DBC,∠BDC=∠AO1O2,根据等腰三角形的性质得出∠BDC=∠CBD即可.
∠AO1B=∠AMB,根据圆内接四边形的性质得出∠AMB=∠BDC,即可判断;②证△BDC∽△AO1O2即可;③无法证出BD=DC,即可判断③;④由△BDC∽△AO1O2,得出∠O2AO1=∠DBC,∠BDC=∠AO1O2,根据等腰三角形的性质得出∠BDC=∠CBD即可.
解答: 解:延长O2O1交圆O1于M,连接AB、AM、BM、O2B,
解:延长O2O1交圆O1于M,连接AB、AM、BM、O2B,
∵圆O1与圆O2交于A、B,
∴O2O1是AB的垂直平分线,
∵O1A=O1B,
∴∠AO1O2= ∠AO1B=∠AMB,
∠AO1B=∠AMB,
∵四边形AMBD是圆O1的内接四边形,
∴∠AMB=∠BDC,
∴①正确;
∵O1A=O1B,
∴∠C= ∠AO2B=∠AO2M,∠AO1O2=∠AMB,
∠AO2B=∠AO2M,∠AO1O2=∠AMB,
∴△BDC∽△AO1O2,
∴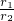 =
=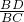 ,
,
∴②正确;
∵△BDC∽△AO1O2,
∴∠O2AO1=∠DBC,∠BDC=∠AO1O2,
∵O2A=O2B,
∴∠AO1O2=∠O2AO1,
∴∠DBC=∠BDC,
∴DC=BC,∴④正确;
无法证出∠C=∠DBC,
即BD≠DC,
∵AD=BD,
∴③错误.
故答案为:①②④.
点评:本题主要考查对相似三角形的性质和判定,等腰三角形的性质和判定,相交两圆的性质,圆的内接四边形的性质,圆周角定理,线段的垂直平分线性质等知识点的理解和掌握,综合运用这些性质进行证明是证此题的关键,题型较好,难度适中.
分析:①延长O2O1交圆O1于M,连接AB、AM、BM、O2B,根据相交两圆的性质推出O2O1是AB的垂直平分线,得出∠AO1O2=
 ∠AO1B=∠AMB,根据圆内接四边形的性质得出∠AMB=∠BDC,即可判断;②证△BDC∽△AO1O2即可;③无法证出BD=DC,即可判断③;④由△BDC∽△AO1O2,得出∠O2AO1=∠DBC,∠BDC=∠AO1O2,根据等腰三角形的性质得出∠BDC=∠CBD即可.
∠AO1B=∠AMB,根据圆内接四边形的性质得出∠AMB=∠BDC,即可判断;②证△BDC∽△AO1O2即可;③无法证出BD=DC,即可判断③;④由△BDC∽△AO1O2,得出∠O2AO1=∠DBC,∠BDC=∠AO1O2,根据等腰三角形的性质得出∠BDC=∠CBD即可.解答:
 解:延长O2O1交圆O1于M,连接AB、AM、BM、O2B,
解:延长O2O1交圆O1于M,连接AB、AM、BM、O2B,∵圆O1与圆O2交于A、B,
∴O2O1是AB的垂直平分线,
∵O1A=O1B,
∴∠AO1O2=
 ∠AO1B=∠AMB,
∠AO1B=∠AMB,∵四边形AMBD是圆O1的内接四边形,
∴∠AMB=∠BDC,
∴①正确;
∵O1A=O1B,
∴∠C=
 ∠AO2B=∠AO2M,∠AO1O2=∠AMB,
∠AO2B=∠AO2M,∠AO1O2=∠AMB,∴△BDC∽△AO1O2,
∴
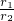 =
=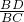 ,
,∴②正确;
∵△BDC∽△AO1O2,
∴∠O2AO1=∠DBC,∠BDC=∠AO1O2,
∵O2A=O2B,
∴∠AO1O2=∠O2AO1,
∴∠DBC=∠BDC,
∴DC=BC,∴④正确;
无法证出∠C=∠DBC,
即BD≠DC,
∵AD=BD,
∴③错误.
故答案为:①②④.
点评:本题主要考查对相似三角形的性质和判定,等腰三角形的性质和判定,相交两圆的性质,圆的内接四边形的性质,圆周角定理,线段的垂直平分线性质等知识点的理解和掌握,综合运用这些性质进行证明是证此题的关键,题型较好,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 24、如图,已知⊙O1与⊙O2相交于A、B两点,连心线O1O2交⊙O1于C、D两点,直线CA交⊙O2于点P,直线PD交⊙O1于点Q,且CP∥QB,求证:AC=AP.
24、如图,已知⊙O1与⊙O2相交于A、B两点,连心线O1O2交⊙O1于C、D两点,直线CA交⊙O2于点P,直线PD交⊙O1于点Q,且CP∥QB,求证:AC=AP.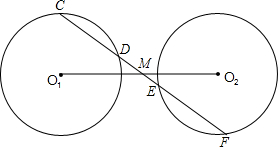 助线或另添字母),则M是线段O1O2的中点,并说明理由.(说明理由时可添加辅助线或字母)
助线或另添字母),则M是线段O1O2的中点,并说明理由.(说明理由时可添加辅助线或字母) 如图,已知⊙O1与⊙O2相交于A、B两点,过A作⊙O1的切线交⊙O2于E,连接EB并延长交⊙O1于C,直线CA交⊙O2于点D.
如图,已知⊙O1与⊙O2相交于A、B两点,过A作⊙O1的切线交⊙O2于E,连接EB并延长交⊙O1于C,直线CA交⊙O2于点D. 如图,已知⊙O1与⊙O2相交于点A、B,AB=8,O1O2=1,⊙O1的半径长为5,那么⊙O2的半径长为
如图,已知⊙O1与⊙O2相交于点A、B,AB=8,O1O2=1,⊙O1的半径长为5,那么⊙O2的半径长为 如图,已知⊙O1与⊙O2的半径分别为r1,r2,⊙O2经过⊙O1的圆心O1,且两圆相交于A,B两点,C为⊙O2上的点,连接AC交⊙O1于D点,再连接BC,BD,AO1,AO2,O1O2,有如下四个结论:①∠BDC=∠AO1O2;②
如图,已知⊙O1与⊙O2的半径分别为r1,r2,⊙O2经过⊙O1的圆心O1,且两圆相交于A,B两点,C为⊙O2上的点,连接AC交⊙O1于D点,再连接BC,BD,AO1,AO2,O1O2,有如下四个结论:①∠BDC=∠AO1O2;②