Question

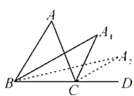
【题目】如图，在△ABC中，∠A＝m°，∠ABC和∠ACD的平分线交于点A1，得∠A1，∠A1BC和∠A1CD的平分线交于点A2，得∠A2…∠A2 017BC和∠A2 017CD的平分线交于点A2 018，则∠A2 018＝_____度．

Answer 1

【答案】

【解析】根据三角形的一个外角等于与它不相邻的两个内角的和和可得∠A+∠ABC=∠ACD，∠A1+∠A1BC=∠A1CD，根据角平分线的定义可得∠A1BC=∠ABC，∠A1CD=∠ACD，然后整理即可得到∠A1=∠A；同理可得后一个角是前一个角的，然后写出∠A2013与∠A的关系，即可得解．（2）同理可得后一个角是前一个角的，然后写出∠A2013与∠A的关系，即可得解．

由三角形的外角性质得，∠A+∠ABC=∠ACD，∠A1+∠A1BC=∠A1CD，

∵∠ABC和∠ACD的平分线交于点A1，

∴∠A1BC=∠ABC，∠A1CD=∠ACD，

∴∠A1+∠A1BC=（∠A+∠ABC），

∴∠A1=∠A，

∵∠A=m°，

∴∠A1=m°；

同理可得：∠A2=∠A1=∠A，

∠A3=∠A2=∠A，

…，

∠A2018=∠A，

∵∠A=m°，

∴∠A2018=．

故答案为：．