题目内容
【题目】
已知:如图(1),在平面直角坐标系中,点![]() ,
,![]() ,
,![]() 分别在坐标轴上,且
分别在坐标轴上,且![]() ,
,![]() 的面积为
的面积为![]() ,点
,点![]() 从
从![]() 点出发沿
点出发沿![]() 轴负方向以
轴负方向以![]() 个单位长度/秒的速度向下运动,连接
个单位长度/秒的速度向下运动,连接![]() ,
,![]() ,点
,点![]() 为
为![]() 上的中点.
上的中点.
(1)直接写出坐标![]() ___________,
___________,![]() ___________,
___________,![]() ___________.
___________.
(2)设点![]() 运动的时间为
运动的时间为![]() 秒,问:当
秒,问:当![]() 与
与![]() 垂直且相等时,求此时
垂直且相等时,求此时![]() 的值?并说明理由.
的值?并说明理由.
(3)如图(2)![]() ,在第四象限内有一动点
,在第四象限内有一动点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,点
,点![]() 在第四象限内运动,当
在第四象限内运动,当![]() ,判断
,判断![]() 是否平分
是否平分![]() ,并说明理由.
,并说明理由.

【答案】(1)(-4,0),(4,0),(0,-4);(2)当t=2时,DP与DB垂直且相等,理由见详解;(3)QA平分∠PQB,见详解.
【解析】
(1)根据三角形的面积公式计算,分别求出OA,OB,OC,得到点A,B,C的坐标;
(2)作DM⊥x轴于点M,作DN⊥y轴于点N,根据勾股定理用t表示出DB,DP,PB,然后再根据勾股定理列出方程,解方程即可;
(3)根据等边三角形的判定和性质得到∠APB=60°,进而得到A,B,Q,P四点共圆,再根据圆周角定理解答.
解:(1)∵OA=OB=OC,
∴AB=2OA,
∵∠AOC=90°,△ABC的面积为16,
∴![]() ×AB×OC=16,即
×AB×OC=16,即![]() ×2OA×OC=16,
×2OA×OC=16,
∴OA=OC=OB=4,
∴A(-4,0),B(4,0),C(0,-4),
(2)当t=2秒时,即CP=OC时,DP与DB垂直且相等.
理由如下:作DM⊥x轴于点M,作DN⊥y轴于点N,
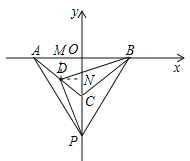
则OM∥OC,DN∥OA,
∵D为线段AC中点,
∴DM=2,OM=2,DN=2,NC=2,
∴BD2=DM2+BM2=40.
∴DP2=DN2+PN2=4+(2+2t)2=8+8t+4t2,PB2=OB2+PO2=16+(4+2t)2=32+16t+4t2,
当DP与DB垂直时,有40+8+8t+4t2=32+16t+4t2,
解得,t=2,
当t=2时,8+8t+4t2=40,
∴DP=DB,
∴当t=2时,DP与DB垂直且相等;
(3)QA平分∠PQB,
理由:∵OA=OB,PO⊥AB,
∴PA=PB,又∠ABP=60°,
∴△PAB为等边三角形,
∴∠APB=60°,
∵∠ABP=60°,∠PQA=60°,
∴∠ABP=∠PQA,
∴A,B,Q,P四点共圆,
∴∠AQB=∠APB=60°,
∴∠AQB=∠AQP,即QA平分∠PQB.

【题目】寒假即将到来,某校为了解学生假期“最喜欢的健身项目”的情况,随机抽取了部分学生进行问卷调查,规定每人从“篮球”、“羽毛球”、“自行车”“爬山”和“其他”五个选项中必须选择且只能选择一个,并将调查结果绘制成如下两幅不完整的统计图表.
最喜爱的健身项目人数调查统计表
最喜爱的项目 | 人数 |
篮球 | 20 |
羽毛球 | 9 |
自行车 | 10 |
爬山 | a |
其他 | b |
合计 |
根据以上信息,请回答下列问题:

(1)这次调查的学生一共有多少人?并求a+b的值.
(2)扇形统计图中,“自行车”对应的扇形的圆心角为 度.
(3)结合自身的寒假健身计划,从以上五个选项中选择你所喜欢的一项健身项目是 .






