Ő‚ńŅńŕ»›
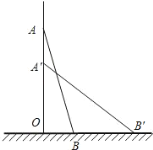
°ĺŐ‚ńŅ°Ņ‘ŕĶ»—Ł°ųOABļÕĶ»—Ł°ųOCD÷–£¨OA£ĹOB£¨OC£ĹOD£¨Ń¨Ĺ”AC°ĘBDĹĽ”ŕĶ„M£ģ

£®1£©»ÁÕľ1£¨»Ű°ŌAOB£Ĺ°ŌCOD£Ĺ40°„£ļ
ĘŔAC”ŽBDĶń żŃŅĻōŌĶő™°° °°£Ľ
Ęŕ°ŌAMBĶń∂» żő™°° °°£Ľ
£®2£©»ÁÕľ2£¨»Ű°ŌAOB£Ĺ°ŌCOD£Ĺ90°„£ļ
ĘŔŇ–∂ŌAC”ŽBD÷ģľšīś‘ŕ‘ű—ýĶń żŃŅĻōŌĶ£Ņ≤ĘňĶ√ųņŪ”…£Ľ
Ęŕ«ů°ŌAMBĶń∂» ż£Ľ
£®3£©‘ŕ£®2£©ĶńŐűľĢŌ¬£¨ĶĪ°ŌCAB£Ĺ30°„£¨«“Ķ„C”ŽĶ„M÷ōļŌ Ī£¨«Ž÷ĪĹ”–ī≥ŲOD”ŽOA÷ģľšīś‘ŕĶń żŃŅĻōŌĶ£ģ
°ĺīūįł°Ņ£®1£©ĘŔAC£ĹBD£ĽĘŕ40°„£Ľ£®2£©ĘŔAC£ĹBD£¨ņŪ”…ľŻĹ‚őŲ£ĽĘŕ90°„£Ľ£®3£©OD£Ĺ![]() OAĽÚOD£Ĺ
OAĽÚOD£Ĺ![]() OA
OA
°ĺĹ‚őŲ°Ņ
£®1£©÷§√ų°ųBOD°’°ųAOC£¨Ķ√AC=BD£¨°ŌOBD£Ĺ°ŌOAC£¨‘ŔņŻ”√ńŕĹ«ļÕ∂®ņŪ«ů°ŌAMBĶń∂» ż£Ľ
£®2£©ņŗĪ»£®1£©÷§√ų°ųBOD°’°ųAOC£¨Ķ√AC=BD£¨°ŌOBD£Ĺ°ŌOAC£¨‘ŔņŻ”√ńŕĹ«ļÕ∂®ņŪ«ů°ŌAMBĶń∂» ż£Ľ
£®3£©łýĺ›ŐűľĢŅ…÷™D°ĘB°ĘC»żĶ„Ļ≤ŌŖ£¨Ľ≠≥ŲŃĹ÷÷«ťŅŲĶńÕľ–ő£¨ņŻ”√£®2£©÷–ĹŠ¬Řľįłýĺ›30°„Ĺ«ňý∂‘Ķń÷ĪĹ«ĪŖĶ»”ŕ–ĪĪŖĶń“ĽįŽļÕĻīĻ…∂®ņŪĹęAC°ĘBCĺý”√ABĪŪ ĺ£¨ĹÝ∂ÝÕ∆≥ŲCD”ŽABĶńĻōŌĶ£¨‘Ŕłýĺ›CD=![]() OD£¨AB=
OD£¨AB=![]() OA,ľīŅ…Ķ√≥ŲOD”ŽOAĶń żŃŅĻōŌĶ
OA,ľīŅ…Ķ√≥ŲOD”ŽOAĶń żŃŅĻōŌĶ
£®1£©»ÁÕľ1ňý ĺ£¨
ĘŔ°Ŗ°ŌAOB£Ĺ°ŌCOD
°ŗ°ŌAOB+°ŌAOD£Ĺ°ŌCOD+°ŌAOD
°ŗ°ŌBOD£Ĺ°ŌAOC
‘ŕ°ųBODļÕ°ųAOC÷–

°ŗ°ųBOD°’°ųAOC£®SAS£©
°ŗAC£ĹBD.
Ļ īūįłő™£ļAC£ĹBD£Ľ
Ęŕ°Ŗ°ųBOD°’°ųAOC
°ŗ°ŌOBD£Ĺ°ŌOAC
°Ŗ°ŌAOB£Ĺ40°„£¨
°ŗ°ŌOAB+°ŌOBA£Ĺ180°„©Ā°ŌAOB£Ĺ180°„©Ā40°„£Ĺ140°„
”÷°Ŗ°ŌOAB+°ŌOBA£Ĺ°ŌOAB+°ŌABD+°ŌOBD
°ŗ°ŌOAB+°ŌOBA£Ĺ°ŌOAB+°ŌABD+°ŌOAC£Ĺ140°„£¨
°ŗ°ŌMAB+°ŌABM£Ĺ140°„
°Ŗ‘ŕ°ųABM÷–£¨°ŌAMB+°ŌMAB+ABM£Ĺ180°„£¨
°ŗ°ŌAMB£Ĺ40°„
Ļ īūįłő™£ļ40°„£Ľ
£®2£©»ÁÕľ2ňý ĺ£¨
ĘŔAC£ĹBD£¨
°Ŗ°ŌAOB£Ĺ°ŌCOD£Ĺ90°„£¨
°ŗ°ŌAOB+°ŌAOD£Ĺ°ŌCOD+°ŌAOD£¨
°ŗ°ŌBOD£Ĺ°ŌAOC£¨
‘ŕ°ųBODļÕ°ųAOC÷–
 £¨
£¨
°ŗ°ųBOD°’°ųAOC£®SAS£©
°ŗBD£ĹAC
Ęŕ°Ŗ°ųBOD°’°ųAOC£¨
°ŗ°ŌOBD£Ĺ°ŌOAC£¨
”÷°Ŗ°ŌOAB+°ŌOBA£Ĺ90°„£¨
°ŌABO£Ĺ°ŌABM+°ŌOBD£¨
°ŌMAB£Ĺ°ŌMAO+°ŌOAB£¨
°ŗ°ŌMAB+°ŌMBA£Ĺ90°„£¨
”÷°Ŗ‘ŕ°ųAMB÷–£¨°ŌAMB+°ŌABM+°ŌBAM£Ĺ180°„£¨
°ŗ°ŌAMB£Ĺ180°„©Ā£®°ŌABM+°ŌBAM£©£Ĺ180°„©Ā90°„£Ĺ90°„£Ľ
£®3£©»ÁÕľ3ňý ĺ£¨°ŌAOB£Ĺ°ŌCOD£Ĺ90°„£¨OA£ĹOB£¨OC£ĹOD£¨°ŌCAB£Ĺ30°„£¨
°ŗ°ŌOAB£Ĺ°ŌOBA£Ĺ°ŌOCD£Ĺ°ŌODC£Ĺ45°„£¨AB£Ĺ![]() OA£¨CD£Ĺ
OA£¨CD£Ĺ![]() OC£¨
OC£¨
”…£®2£©Ķ√°ųBOD°’°ųAOC£®SAS£©
°ŗ°ŌACO£Ĺ°ŌBDO£Ĺ45°„£¨BD£ĹAC
°ŗ°ŌACD£Ĺ°ŌACO+°ŌOCD£Ĺ90°„
°ŗ°ŌACB£Ĺ90°„
°ŗBC£Ĺ![]() AB
AB
”…ĻīĻ…∂®ņŪĶ√£ļAC£Ĺ![]() £Ĺ
£Ĺ![]() AB
AB
°ŗCD£ĹAC©ĀBC£Ĺ![]() AB
AB
°ŗ![]() OC£Ĺ
OC£Ĺ![]() °Ń
°Ń![]() OA
OA
°ŗOD£ĹOC£Ĺ![]() OA£ģ
OA£ģ
»ÁÕľ4£¨Õ¨…Ō”…ĻīĻ…∂®ņŪĶ√£ļAC£Ĺ![]() £Ĺ
£Ĺ![]() AB
AB
°ŗCD£ĹAC+BC£Ĺ![]() AB
AB
°ŗ![]() OC£Ĺ
OC£Ĺ![]() °Ń
°Ń![]() OA
OA
°ŗOD£ĹOC£Ĺ![]() OA£ģ
OA£ģ
◊Ř…Ōňý Ų£¨OD£Ĺ![]() OAĽÚOD£Ĺ
OAĽÚOD£Ĺ![]() OA£ģ
OA£ģ





 √Ż ¶Ķ„ĺ¶◊÷ī ĺš∂ő∆™ŌĶŃ–īūįł
√Ż ¶Ķ„ĺ¶◊÷ī ĺš∂ő∆™ŌĶŃ–īūįł