题目内容
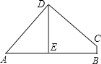
【题目】如图,已知△ABC中,AD是BC边上的高,CE平分∠ACB,AD与CE相交于点F.∠B=65°,∠AFC=120°,求∠BAD和∠ACB的度数.

【答案】∠BAD的度数是25°,∠ACB的度数是60°
【解析】
在△ABD中根据∠B和∠ADB的度数即可求出∠BAD的度数;根据外角性质可得∠FCD的度数,利用角平分线的性质即可得出∠ACB的度数.
解:∵AD是BC边上的高
∴∠ADB=90°
在Rt△ABD中,∠BAD=90°-∠B=90°-65°=25°
∠AFC是ΔCDF的外角
即∠AFC=∠FDC+∠FCD
∴∠FCD=∠AFC-∠FDC=120°-90°=30°
∴CE平分∠ACB
∴∠ACB=2∠FCD=2×30°=60°
答:∠BAD的度数是25°,∠ACB的度数是60°.


练习册系列答案
相关题目