题目内容
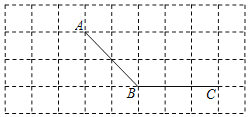
【题目】如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点![]() 到点E,使
到点E,使![]() ,然后以OG、OE为邻边作正方形OEFG,连接
,然后以OG、OE为邻边作正方形OEFG,连接![]() .
.
![]() 求证:
求证:![]() ;
;
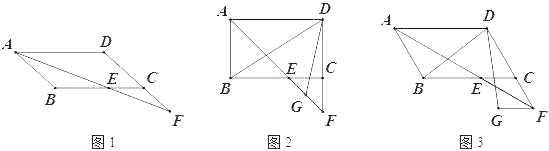
![]() 正方形ABCD固定,将正方形OEFG绕点O逆时针旋转
正方形ABCD固定,将正方形OEFG绕点O逆时针旋转![]() 角
角![]() 得到正方形
得到正方形![]() ,如图2.
,如图2.
![]() 在旋转过程中,当
在旋转过程中,当![]() 是直角时,求
是直角时,求![]() 的度数;
的度数;
![]() 若正方形ABCD的边长为1,在旋转过程中,求
若正方形ABCD的边长为1,在旋转过程中,求![]() 长的最大值和此时
长的最大值和此时![]() 的度数,直接写出结果不必说明理由.
的度数,直接写出结果不必说明理由.

【答案】(1)见解析;(2)![]() ;
;![]()
【答题空27-1】![]()
【答题空27-2】![]()
【解析】分析:(1)延长ED交AG于点H,证明![]() ≌
≌![]() ,根据等量代换证明结论;
,根据等量代换证明结论;
(2)根据题意和锐角正弦的概念以及特殊角的三角函数值得到![]() ,分两种情况求出
,分两种情况求出![]() 的度数;
的度数;
(3)根据正方形的性质分别求出OA和OF的长,根据旋转变换的性质求出AF′长的最大值和此时![]() 的度数.
的度数.
详解:![]() 如图1,延长ED交AG于点H,
如图1,延长ED交AG于点H,
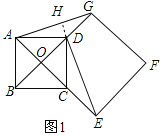
![]() 点O是正方形ABCD两对角线的交点,
点O是正方形ABCD两对角线的交点,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
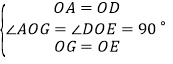 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即![]() ;
;
![]() 在旋转过程中,
在旋转过程中,![]() 成为直角有两种情况:
成为直角有两种情况:
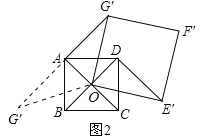
![]() Ⅰ
Ⅰ![]() 由
由![]() 增大到
增大到![]() 过程中,当
过程中,当![]() 时,
时,
![]() ,
,
![]() 在
在![]() 中,sin∠AGO=
中,sin∠AGO=![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即![]() ;
;
![]() Ⅱ
Ⅱ![]() 由
由![]() 增大到
增大到![]() 过程中,当
过程中,当![]() 时,
时,
同理可求![]() ,
,
![]() .
.
综上所述,当![]() 时,
时,![]() 或
或![]() .
.
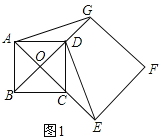
![]() 如图3,
如图3,
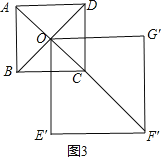
当旋转到A、O、![]() 在一条直线上时,
在一条直线上时,![]() 的长最大,
的长最大,
![]() 正方形ABCD的边长为1,
正方形ABCD的边长为1,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 此时
此时![]() .
.

【题目】某装修公司为某新建小区的A、B两种户型(共300套)装修地板
(1)若A种户型所需木地板、地板砖各为50m2、20m2,B种户型所需木地板、地板砖各为40m2、25m2.公司最多可提供木地板13000m2,最多可提供地板砖7010m2,在此条件下,则可能装修A、B两种户型各多少套?
(2)小王在该小区购买了一套A户型套房(地面总面积为70m2).现有两种铺设地面的方案:①卧室铺实木地板,卧室以外铺亚光地板砖;②卧室铺强化木地板,卧室以外铺抛光地板砖.经预算,铺1m2地板的平均费用如下表.设卧室地面面积为am2,怎样选择所需费用更低?
类别 | 抛光地板砖 | 亚光地板砖 | 实木地板 | 强化木地板 |
平均费用(元/m2) | 170 | 90 | 200 | 80 |