题目内容
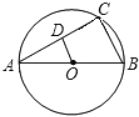
【题目】如图,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于D,BC=4cm.
(1)求证:AC⊥OD;
(2)求OD的长;
(3)若2sinA﹣1=0,求⊙O的直径.
【答案】(1)见解析;(2)OD=2cm;(3)⊙O的直径是8cm.
【解析】
(1)根据圆周角定理即可证明;(2)中位线定理与垂径定理即可得出OD=![]() ;(3)根据2sinA﹣1=0,得出∠A=30°,再根据三角函数的性质即可求解.
;(3)根据2sinA﹣1=0,得出∠A=30°,再根据三角函数的性质即可求解.
(1)证明:∵AB是⊙O的直径,
∴∠C=90°.
∵OD∥BC,
∴∠ADO=∠C=90°.
∴AC⊥OD.
(2)∵OD∥BC,O是AB的中点,
∴OD是△ABC的中位线,
∴点D是AC的中点,
∴OD=![]() BC=
BC=![]() ×4=2cm;
×4=2cm;
(3)∵2sinA﹣1=0,
∴sinA=![]() .
.
∴∠A=30°.
在Rt△ABC中,∠A=30°,
∴BC=![]() AB.
AB.
∴AB=2BC=8(cm).
即⊙O的直径是8cm.

练习册系列答案
相关题目