题目内容
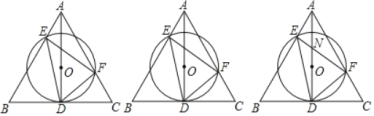
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC边于点D,E是边BC的中点,连接DE、OD,
(1)求证:直线DE是⊙O的切线;
(2)连接OC交DE于F,若OF=FC,试判断△ABC的形状,并说明理由;
(3)若![]() ,求⊙O的半径.
,求⊙O的半径.
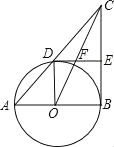
【答案】(1)见解析;(2)等腰直角三角形,理由见解析;(3)3.
【解析】
(1)求出∠CDB=90°,推出DE=BE,得到∠EDB=∠EBD,∠ODB=∠OBD,推出∠ODE=90°即可;
(2)连接OE,证正方形DEBO,推出OB=BE,推出∠EOB=45°,根据平行线的性质推出∠A=45°即可;
(3)设AD=x,CD=2x,证△CDB∽△CBA,得到比例式,代入求出AB即可.
解:如右图所示,连接BD,
(1)∵AB是直径,
∴∠ADB=90°,
∵O是AB的中点,
∴OA=OB=OD,
∴∠OAD=∠ODA,∠ODB=∠OBD,
同理在Rt△BDC中,E是BC的中点,
∴∠EDB=∠EBD,
∵∠OAD+∠ABD=90°,∠ABD+∠CBD=90°,
∴∠OAD=∠CBD,
∴∠ODA=∠EBD,
又∵∠ODA+∠ODB=90°,
∴∠EBD+∠ODB=90°,
即∠ODE=90°,
∴DE是⊙O的切线.
(2)答:△ABC的形状是等腰直角三角形.
理由是:∵E、F分别是BC、OC的中点,
∴EF是三角形OBC的中位线,
∴EF∥AB,
DE⊥BC,
OB=OD,四边形OBED是正方形,
连接OE,
OE是△ABC的中位线,OE∥AC,
∠A=∠EOB=45度,
∴∠A=∠ACB=45°,
∵∠ABC=90°,
∴△ACB是等腰直角三角形.
(3)设AD=x,CD=2x,
∵∠CDB=∠CBA=90°,∠C=∠C,
∴△CDB∽△CBA,
∴![]() ,
,
∴![]() ,
,
x=2![]() ,
,
AC=6![]() ,
,
由勾股定理得:AB=![]() =6,
=6,
∴圆的半径是3.
答:⊙O的半径是3.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案