题目内容
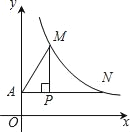
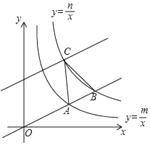
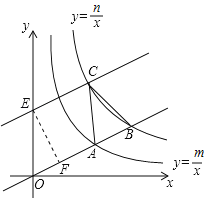
【题目】如图,直线y=![]() x分别与双曲线y=
x分别与双曲线y=![]() (m>0,x>0),双曲线y=
(m>0,x>0),双曲线y=![]() (n>0,x>0)交于点A和点B,且
(n>0,x>0)交于点A和点B,且![]() ,将直线y=
,将直线y=![]() x向左平移6个单位长度后,与双曲线y=
x向左平移6个单位长度后,与双曲线y=![]() 交于点C,若S△ABC=4,则
交于点C,若S△ABC=4,则![]() 的值为_____,mn的值为_____.
的值为_____,mn的值为_____.
【答案】![]() 100
100
【解析】
先求出直线y=![]() x向左平移6个单位长度后的解析式为y=
x向左平移6个单位长度后的解析式为y=![]() x+4,那么直线y=
x+4,那么直线y=![]() x+4交y轴于E(0,4),作EF⊥OB于F.根据互相垂直的两直线斜率之积为﹣1得出直线EF的解析式为y=﹣
x+4交y轴于E(0,4),作EF⊥OB于F.根据互相垂直的两直线斜率之积为﹣1得出直线EF的解析式为y=﹣![]() x+4,再求出F点的坐标,根据勾股定理求得EF,根据S△ABC=4,求出AB,那么根据
x+4,再求出F点的坐标,根据勾股定理求得EF,根据S△ABC=4,求出AB,那么根据![]()
![]() ,求得OA,进而求出A、B两点坐标,求出m、n即可解决问题.
,求得OA,进而求出A、B两点坐标,求出m、n即可解决问题.
解:直线y=![]() x向左平移6个单位长度后的解析式为y=
x向左平移6个单位长度后的解析式为y=![]() (x+6),即y=
(x+6),即y=![]() x+4,
x+4,
∴直线y=![]() x+4交y轴于E(0,4),作EF⊥OB于F.
x+4交y轴于E(0,4),作EF⊥OB于F.
可得直线EF的解析式为y=﹣![]() x+4,
x+4,
由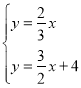 ,解得
,解得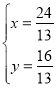 ,即
,即![]() .
.
∴EF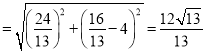 ,
,
∵S△ABC=4,
∴![]() ABEF=4,
ABEF=4,
∴AB![]() ,
,
∵![]() ,
,
∴OA=![]() AB=
AB=![]() ,
,
∴A(3,2),B(5,![]() ),
),
∴m=6,n=![]() ,
,
∴![]() ,mn=100.
,mn=100.
故答案是:![]() ,100.
,100.

练习册系列答案
相关题目