题目内容
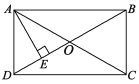
【题目】如图,在矩形ABCD中,对角线AC与BD交于点O,且△ADO为等边三角形,过点A作AE⊥BD于点E.
(1)求∠ABD的度数;
(2)若BD=10,求AE的长.
【答案】(1)∠ABD=30°;(2)AE=![]() .
.
【解析】
(1)根据矩形性质得出∠DAB=90°,求出∠ADB=60°,代入∠ABD=180°-∠DAB-∠ADB求出即可;
(2)求出AD,根据等腰三角形性质得出DE=EO,求出DE,根据勾股定理求出即可.
(1)∵四边形ABCD是矩形,∴∠DAB=90°,
∵△ADO为等边三角形,∴∠ADB=60°,
∴∠ABD=180°-∠DAB-∠ADB=30°;
(2)∵BD=10,∠BAD=90°,∠ABD=30°,
∴AD=![]() BD=5,
BD=5,
∵△ADO为等边三角形,∴AD=AO=DO=5,
∵AE⊥DO,∴DE=EO=![]() DO=2.5,
DO=2.5,
在Rt△AED中,由勾股定理得AE=![]() .
.

练习册系列答案
相关题目
【题目】某商店分两次购进![]() 、
、![]() 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量(件) | 购进所需费用(元) | ||
|
| ||
第一次 | 30 | 40 | 3800 |
第二次 | 40 | 30 | 3200 |
(1)求![]() 、
、![]() 两种商品每件的进价分别是多少元?
两种商品每件的进价分别是多少元?
(2)商场决定![]() 种商品以每件30元出售,
种商品以每件30元出售,![]() 种商品以每件100元出售.为满足市场需求,需购进
种商品以每件100元出售.为满足市场需求,需购进![]() 、
、![]() 两种商品共1000件,且
两种商品共1000件,且![]() 种商品的数量不少于
种商品的数量不少于![]() 种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.