题目内容
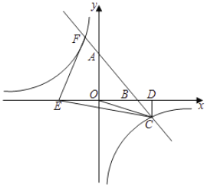
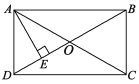
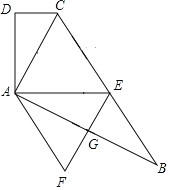
【题目】如图,在四边形![]() 中,
中,![]() 平分
平分![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,过
,过![]() 作
作![]() 于
于![]() ,并延长
,并延长![]() 至点
至点![]() ,使
,使![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求证:四边形
,求证:四边形![]() 是菱形.
是菱形.
【答案】(1)见详解;(2)见详解
【解析】
(1)欲证明AC2=CDBC,只需推知△ACD∽△BCA即可;
(2)利用“在直角三角形中,30度角所对的直角边等于斜边的一半”、“直角三角形斜边上的中线等于斜边的一半”推知四边形AKEC的四条边都相等,则四边形AKEC是菱形.
证明:(1)∵AC平分∠BCD,
∴∠DCA=∠ACB.
又∵AC⊥AB,AD⊥AE,
∴∠DAC+∠CAE=90°,∠CAE+∠EAB=90°,
∴∠DAC=∠EAB.
又∵E是BC的中点,
∴AE=BE,
∴∠EAB=∠ABC,
∴∠DAC=∠ABC,
∴△ACD∽△BCA,
∴![]() ,
,
∴AC2=CDBC;
(2)证明:∵EF⊥AB,AC⊥AB,
∴EF∥AC,
又∵∠B=30°,
∴AC=![]() BC=EB=EC.
BC=EB=EC.
又EF=EB,
∴EF=AC,
即AF=FE=EC=CA,
∴四边形AFEC是菱形.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
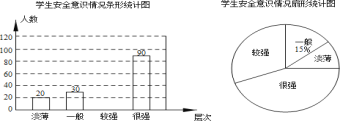
【题目】为了让同学们了解自己的体育水平,八年级1班的体育老师对全班50名学生进行了一次体育模拟测试(得分均为整数).成绩满分为10分,1班的体育委员根据这次测试成绩制作了如下的统计图:

(1)根据统计图所给的信息填写下表:
平均数(分) | 中位数(分) | 众数(分) | |
男生 | 8 | ||
女生 | 8 | 8 |
(2)若女生队测试成绩的方差为1.76,请计算男生队测试成绩的方差.并说明在这次体育测试中,哪个队的测试成绩更整齐些?