题目内容
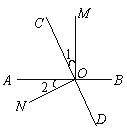
【题目】如图,直线AB,CD相交于O点,OM⊥AB.
(1)若∠1=∠2,求∠NOD;
(2)若∠1=![]() ∠BOC,求∠AOC与∠MOD.
∠BOC,求∠AOC与∠MOD.
【答案】(1)90°;(2)∠AOC=60°,∠MOD=150°.
【解析】(1)根据垂直的定义,可得∠AOC+∠1=90°由此易推出∠CON=90°,进而结合平角的定义即可解答本题;
(2)根据垂直可知∠AOM=∠BOM=90°,结合∠1=![]() ∠BOC,可得∠1=30°,由此可以得到∠AOC与MOD的度数.
∠BOC,可得∠1=30°,由此可以得到∠AOC与MOD的度数.
解:(1)∵OM⊥AB,
∴∠AOM=90°,即∠AOC+∠1=90°.
∵∠1=∠2,∠AOC+∠1=90°,
∴∠AOC+∠2=90°,
即∠CON=90°,
∵∠CON+∠NOD=180°,
∴∠NOD=90°.
(2)∵OM⊥AB,
∴∠AOM=∠BOM=90°.
∵∠BOC=∠BOM+∠1,∠BOM=90°,∠1=![]() ∠BOC,
∠BOC,
∴∠1=30°.
∵∠AOC+∠1=∠AOM=90°,∠1=30°,
∴∠AOC=60°,
∴∠BOD=∠AOC=60°,
∴∠MOD=∠MOB+∠AOC=150°.

练习册系列答案
相关题目