Question

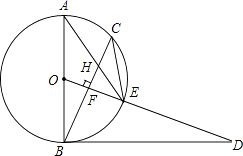
【题目】如图已知∠1＋∠2＝180°，∠3＝∠B，试判断∠AED与∠C的大小关系，并说明理由(根据解题的要求，在横线处或括号内填写适当的内容或理由)．

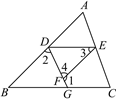
解：∠AED＝∠C.

理由如下：

∵∠1＋∠4＝180°，∠1＋∠2＝180°，

∴∠2＝∠4，∴AB∥EF，

∴________________(两直线平行，内错角相等)．

又∵∠3＝∠B，∴∠B＝∠ADE，

∴DE∥BC(____________________________)，

∴∠AED＝∠C(__________________________)．

Answer 1

【答案】∠3＝∠ADE；同位角相等，两直线平行；两直线平行，同位角相等.

【解析】

根据平行线的判定方法和平行线的性质填空即可．

证明：∵∠1+∠4=180°，∠1+∠2=180°，

∴∠2=∠4，∴AB∥EF，

∴∠3=∠ADE（两直线平行，内错角相等）

∵∠3=∠B，

∴∠B=∠ADE，

∴DE∥BC（ 同位角相等两直线平行）

∴∠AED=∠C（ 两直线平行，同位角相等）．