题目内容
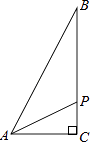
【题目】如图,已知某船于上午8时在A处观测小岛C在北偏东60°方向上,该船以每小时20海里的速度向东航行到B处,测得小岛C在北偏东30°方向上,船以原来的速度继续向东航行2小时,到达岛C正南方点D处,船从A到D一共航行了多少海里?

【答案】船从A到D一共走了120海里.
【解析】
根据直角三角形 30°角所对的直角边等于斜边的一半求出 BC 的长度,再根据两个方位角证明 AB=BC,根据AD=AB+BD即可求解.
由题意知∠CAD=30°,∠CBD=60°,
在△BCD 中,∠CBD=60°,
∴∠BCD=30°,
∴BC=2BD,
∵船从B到D走了2小时,船速为每小时20海里,
∴BD=40 海里,
∴BC=80海里,
由∠CBD=60°,得∠ABC=120°,
∵∠CAD=30°,
∴∠ACB=30°,
∴AB=BC,
∴AB=80海里,
∵AD=AB+BD,
∴AD=80+40=120(海里).
因此船从A到D一共走了120海里.

练习册系列答案
相关题目