题目内容
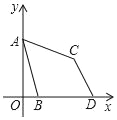
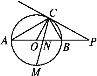
【题目】如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=1,AD=3,DC=5.点S沿A→B→C运动到C点停止,以S为圆心,SD为半径作弧交射线DC于T点,设S点运动的路径长为x,等腰△DST的面积为y,则y与x的函数图象应为( )
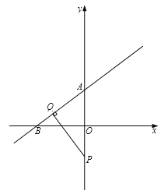
A. 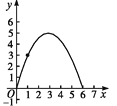 B.
B. 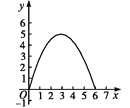
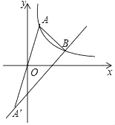
C. 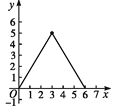 D.
D. 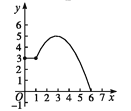
【答案】A
【解析】
分别讨论S在AB边时和BC边时,y与x的函数关系式,结合选项得出结论.
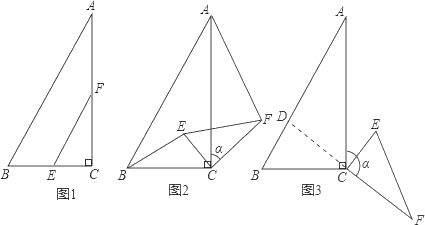
如图:①当S在AB边时,即0≤x≤1时,则AS=x,过S作SE⊥DT于E,
∵∠A=90°,AB//CD
∴四边形ADES是矩形,
∴S△ADS=S△ESD,
∵SD=ST,SE⊥DT
∴S△ESD=S△EST
∴y=S△DST=2S△ESD=2S△ADS=2×![]() ×3x=3x,
×3x=3x,
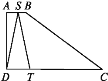
∴0≤x≤1时,y与x是正比例函数关系,图像是过原点的直线,且x=1时,y=3,
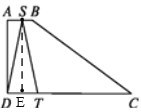
②如图:当S在BC边时,即1<x≤6时,则BS=x-1
过B作BF⊥CD,过S作SN⊥CD,延长NS交AB延长线于M,
∵AB=1,CD=5,
∴CF=4,
∴BC=![]() =5,
=5,
∵AM//CD,
∴∠MBC=∠BCF,
∵∠BFC=∠BMS=90°,∠MBC=∠BCF,
∴△BMS∽△BFC,
∴![]() ,
,
解得:MS=![]() (x-1),BM=
(x-1),BM=![]() (x-1),
(x-1),
∴NS=MN-MS=3-![]() (x-1)=
(x-1)=![]() ,DN=AB+BM=1+
,DN=AB+BM=1+![]() (x-1)=
(x-1)=![]() ,
,
∴y=S△DST=![]() ×2×DN
×2×DN![]() NS=(
NS=(![]() )(
)(![]() )=-
)=-![]() x2+
x2+![]() x+
x+![]() ,
,
∴1<x≤6时,y与x是二次函数关系,图像是抛物线,
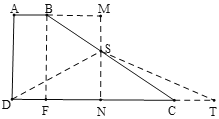
综上所述,只有A选项符合题意,
故选A.

【题目】自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 |
|
| 1.5 |
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利? 说明理由.