Question

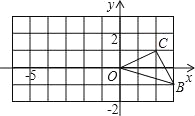
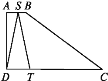
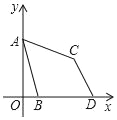
【题目】如图，在平面直角坐标系中，点A（0，3），B是x轴正半轴上一动点，将点A绕点B顺时针旋转60°得点C，OB延长线上有一点D，满足∠BDC＝∠BAC，则线段BD长为_____．

Answer 1

【答案】2．

【解析】

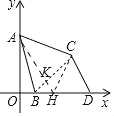
如图，在DO上取一点H，使得DH＝CD．设AH交BC于点K．只要证明△ACH≌△BCD（SAS），推出∠CAH＝∠CBD，AH＝BD，由∠AKC＝∠BKH，推出∠KHB＝∠ACB＝60°，求出AH即可解决问题；

解：如图，在DO上取一点H，使得DH＝CD．设AH交BC于点K．

∵BA＝BC，∠ABC＝60°，

∴△ABC是等边三角形，

∵DC＝DH，∠CDH＝60°，

∴△CDH是等边三角形，

∴CA＝CB，CH＝CD，∠ACB＝∠HCD＝60°，

∴∠ACH＝∠BCD，

∴△ACH≌△BCD（SAS），

∴∠CAH＝∠CBD，AH＝BD，

∵∠AKC＝∠BKH，

∴∠KHB＝∠ACB＝60°，

在Rt△AOH中，∵OA＝3，

∴AH＝＝2，

∴BD＝AH＝2．

故答案为2．