题目内容
如图1,在△ABC中,∠ACB=90°,AC=BC=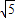 ,以点B为圆心,以
,以点B为圆心,以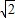 为半径作圆.
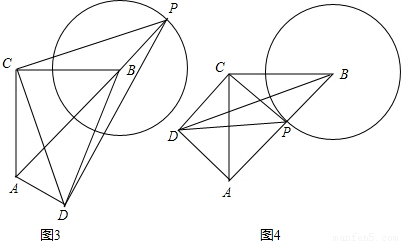
为半径作圆.(1)设点P为⊙B上的一个动点,线段CP绕着点C顺时针旋转90°,得到线段CD,连接DA,DB,PB,如图2.求证:AD=BP;
(2)在(1)的条件下,若∠CPB=135°,则BD=______
【答案】分析:(1)根据SAS即可证明△ACD≌△BCP,再根据全等三角形的性质可得AD=BP;
(2)分P点在BC上面和P点在BC下面两种情况讨论可得BD的长;
(3)当∠PBC=135°时,BD有最大值;当∠PBC=45°时,BD有最小值.
解答: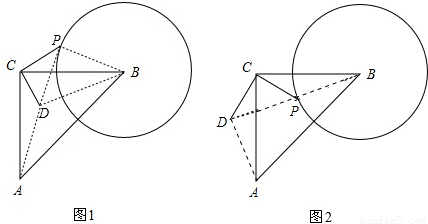 (1)证明:∵∠ACB=90°,∠DCP=90°,
(1)证明:∵∠ACB=90°,∠DCP=90°,
∴∠ACD=∠BCP
在△ACD与△BCP中,
∵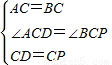 ,
,
∴△ACD≌△BCP(SAS)
∴AD=BP;
(2)解:在(1)的条件下,若∠CPB=135°,则BD=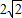 或2;
或2;
(3)解:当∠PBC=135°时,BD有最大值,且最大值为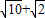 ;
;
当∠PBC=45°时,BD有最小值,且最小值为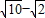 .
.
故答案为: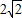 或2;135,
或2;135,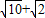 ;45,
;45,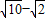 .
.
点评:考查了圆的综合题,涉及的知识有全等三角形的判定与性质,分类思想的运用,最大值与最小值,注意分析问题要全面,以免漏解,有一定的难度.
(2)分P点在BC上面和P点在BC下面两种情况讨论可得BD的长;
(3)当∠PBC=135°时,BD有最大值;当∠PBC=45°时,BD有最小值.
解答:
 (1)证明:∵∠ACB=90°,∠DCP=90°,
(1)证明:∵∠ACB=90°,∠DCP=90°,∴∠ACD=∠BCP
在△ACD与△BCP中,
∵
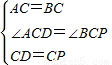 ,
,∴△ACD≌△BCP(SAS)
∴AD=BP;
(2)解:在(1)的条件下,若∠CPB=135°,则BD=
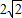 或2;
或2;
(3)解:当∠PBC=135°时,BD有最大值,且最大值为
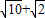 ;
;当∠PBC=45°时,BD有最小值,且最小值为
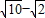 .
.故答案为:
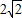 或2;135,
或2;135,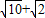 ;45,
;45,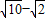 .
.点评:考查了圆的综合题,涉及的知识有全等三角形的判定与性质,分类思想的运用,最大值与最小值,注意分析问题要全面,以免漏解,有一定的难度.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目

 明理由.
明理由.
 如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=
如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=