Question

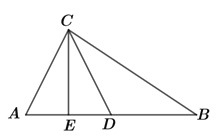
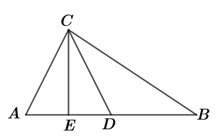
【题目】如图所示．在Rt△ABC中，CD是斜边上的中线，CE是高．已知AB=10cm，DE=2.5cm，则∠BDC=____________度，S△BCD=______cm2．

Answer 1

【答案】120

【解析】

首先根据直角三角形斜边上的中线等于斜边的一半可得CD＝5cm，再根据三角函数值算出∠ECD的度数，然后根据三角形外角的性质可得∠BDC＝∠CED＋∠ECD，进而得到∠BDC的度数；再根据勾股定理可计算出CE的长，然后再利用三角形的面积公式进行计算即可．

∵在Rt△ABC中，CD是斜边上的中线，

∴CD=AB．

∵AB=10cm，

∴CD=5cm．

∵CE是高，

∴△CED是直角三角形．

∵DE=2.5cm，

∴sin∠ECD==，

∴∠ECD=30°，

∴∠BDC=∠CED+∠ECD=90°+30°=120°；

在Rt△CED中：（cm），

∴S△BCD=DBCE=×5×=（cm2）．

故答案为：120；．