题目内容
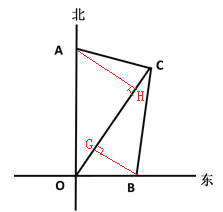
【题目】如图，一条自南向北的大道上有O、A两个景点，O、A相距20km，在O处测得另一景点C位于点O的北偏东37°方向，在A处测得景点C位于点A的南偏东76°方向，且A、C相距13km .
（1）求：①A到OC之间的距离；
②O、C两景点之间的距离；
（2）若在O处测得景点B 位于景点O的正东方向10km，求B、C两景点之间的距离．（参考数据：tan37°=0.75）
【答案】（1）①16km②21km（2）17km
【解析】
(1)①作AH⊥OC于H，解直角三角形AHO即可得解；
②在Rt△AHC中，HC=5，故可求OC的长；
（2）作BG⊥OC于G，可求
，再由勾股定理求出BC即可.
(1)①作AH⊥OC于H，
∵tan∠AOC=0.75，∴
，
设AH=3x，则OH=4x，由勾股定理得，（3x）2+（4x）2=202，
解得，x=4，则AH=12，0H=16km
②在Rt△AHC中，HC=
=5，∴OC=OH+HC=21km
(2) 作BG⊥OC于G，∵∠AOC+∠COB=90°，∠BOC+∠OBG=90°，
∴∠AOC=∠OBG，
∴，又OB=10， ∴OG=6，BG=8，
∴CG=OC﹣OG=15，
∴BC=
=17km
练习册系列答案
相关题目
