题目内容
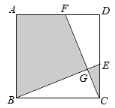
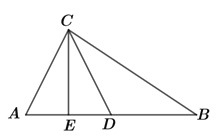
【题目】如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=3,BE=![]() ,求半圆和菱形ABFC的面积.
,求半圆和菱形ABFC的面积.

【答案】(1)见解析;(2) ![]() .
.
【解析】
(1)根据对角线相互平分的四边形是平行四边形,证明是平行四边形,再根据邻边相等的平行四边形是菱形即可证明;
(2)设CD=x,连接BD.利用勾股定理构建方程即可解决问题;
(1)证明:∵AB是直径,
∴∠AEB=90°
∴AE⊥BC,
∵AB=AC,
∴BE=CE,
∵AE=EF,
∴四边形ABFC是平行四边形,
∵AC=AB,
∴四边形ABFC是菱形
(2)设CD=x.连接BD.
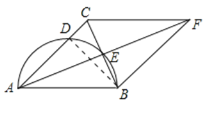
∵AB是直径,
∴∠ADB=∠BDC=90°,
∴AB2-AD2=CB2-CD2,
∴(3+x)2-32=![]() 2-x2,
2-x2,
解得x=2或-5(舍)
∴AB=AC=5,BD=![]()
∴S菱形ABFC=AC×BD=20
∴S半圆=![]() ×π×
×π×![]() π
π

练习册系列答案
相关题目
【题目】某经销商销售一种成本价为10元/kg的商品,已知销售价不低于成本价,且物价部门规定这种产品的销售价不得高于18元/kg.在销售过程中发现销量y(kg)与售价x(元/kg)之间满足一次函数关系,对应关系如下表所示:
x | 12 | 14 | 15 | 17 |
y | 36 | 32 | 30 | 26 |
⑴求y与x之间的函数关系式,并写出自变量x的取值范围;
⑵若该经销商想使这种商品获得平均每天168元的利润,求售价应定为多少元/kg?
⑶设销售这种商品每天所获得的利润为W元,求W与x之间的函数关系式;并求出该商品销售单价定为多少元时,才能使经销商所获利润最大?最大利润是多少?