题目内容
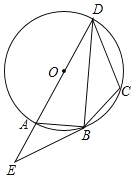
【题目】如图a,已知抛物线y=-![]() x2+bx+c经过点A(4,0) 、C(0,2),与x轴的另一个交点为B.
x2+bx+c经过点A(4,0) 、C(0,2),与x轴的另一个交点为B.
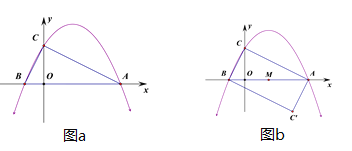
(1)求出抛物线的解析式.
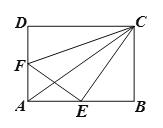
(2)如图b,将△ABC绕AB的中点M旋转180°得到△BAC′,试判断四边形BC′AC的形状.并证明你的结论.
(3)如图a,在抛物线上是否存在点D,使得以A、B、D三点为顶点的三角形与△ABC全等?若存在,请直接写出点D的坐标;若不存在请说明理由.
【答案】(1)y=-![]() x2+
x2+![]() x+2;(2)四边形BC′AC为矩形,见解析;(3)存在,(3,2)
x+2;(2)四边形BC′AC为矩形,见解析;(3)存在,(3,2)
【解析】
(1)由点A、C的坐标,利用待定系数法即可求出抛物线的解析式;
(2)由点A、B、C的坐标可得出OA、OC、OB的长度,利用勾股定理可求出AC、BC的长,由AC2+BC2=25=AB2可得出∠ACB=90°,再利用旋转的性质即可找出四边形BC′AC为矩形;
(3)假设存在这样的点D,设D(x, -![]() x2+
x2+![]() x+2),则有-
x+2),则有-![]() x2+
x2+![]() x+2=2,求出x的值再进行判断即可.
x+2=2,求出x的值再进行判断即可.
(1)∵抛物线y=-![]() x2+bx+c经过点A(4,0) 、C(0,2),
x2+bx+c经过点A(4,0) 、C(0,2),
∴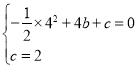
解得,![]()
∴抛物线的解析式为:y=-![]() x2+
x2+![]() x+2
x+2
(2)四边形BC′AC为矩形.
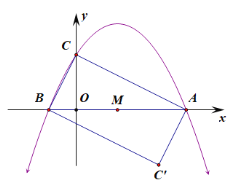
令y=0,则-![]() x2+
x2+![]() x+2=0,解得
x+2=0,解得![]() ,
,![]()
∴B(-1,0)
∵A(4,0) 、C(0,2),
∴OB=1,OA=4,OC=2,
由勾股定理求得:BC=![]() ,AC=2
,AC=2![]()
又AB=5,
∴![]()
∴△ABC直角三角形,∠BCA=90°,
∵△ABC绕AB的中点M旋转
∴四边形BC′AC为平行四边形,
又∠BCA=90°
∴四边形BC′AC为矩形.
(3)设D(x, -![]() x2+
x2+![]() x+2),则有-
x+2),则有-![]() x2+
x2+![]() x+2=2,
x+2=2,
解得,![]() ,
,![]() (不符合题意,舍去),
(不符合题意,舍去),
∴D(3,2)
故存在点D,使得以A、B、D三点为顶点的三角形与△ABC全等.点D的坐标为(3,2).