Question

【题目】如图，矩形AEHC是由三个全等矩形拼成的，AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N，设△BPQ、△DKM、△CNH的面积依次为、、．

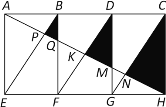
（1）求证：△BPQ∽△DKM∽△CNH；

（2）若，求的值．

Answer 1

【答案】（1）详见解析；（2）16

【解析】

（1）利用矩形的性质，平行四边形的判定与性质，和相似三角形的判定定理进行推理即可；

（2）由条件可以得出△ABP∽△ADK∽△ACN，可以求出△ABP与△ADK的相似比为 ，△ADK与△ACN相似比为，由相似三角形的性质，就可以求出K，从而可以求出S2．

（1）证明：∵矩形AEFB、BFGD、DGHC互相全等，

∴BD=DC=EF=FG，且BD∥EF，DC∥FG，

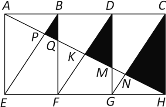
∴四边形BEFD，DFGC为平行四边形，

∴BE∥DF∥CG，

∴∠BPQ=∠DKM=∠CNH，

∵BF∥DG∥CH，

∴∠BQP=∠DMK=∠CHN，

∴△BQP∽△DMK∽△CHN．

（2）∵BP∥DK∥CN，

∴△ABP∽△ADK∽△ACN，

∴，，

由（1）知：△BQP∽△DMK∽△CHN，

∴，，

∴，

设，则，，

∵，∴，

∴，

∴．