题目内容
儿童商场购进一批M型服装,销售时标价为75元/件,按8折销售仍可获利50%.商场现决定对M型服装开展促销活动,每件在8折的基础上再降价x元销售,已知每天销售数量y(件)与降价x(元)之间的函数关系式为y=20+4x(x>0).
(1)求M型服装的进价;
(2)求促销期间每天销售M型服装所获得的利润W的最大值.
(1)求M型服装的进价;
(2)求促销期间每天销售M型服装所获得的利润W的最大值.
(1)设进价为z,
∵销售时标价为75元/件,按8折销售仍可获利50%.
则75×0.8=(1+0.5)z.
∴z=40;
答:M型服装的进价为40元;
(2)∵销售时标价为75元/件,开展促销活动每件在8折的基础上再降价x元销售,
∴M型服装开展促销活动的实际销价为75×0.8-x=60-x,销售利润为60-x-40=20-x.
而每天销售数量y(件)与降价x(元)之间的函数关系式为y=20+4x,
∴促销期间每天销售M型服装所获得的利润:
W=(20-x)(20+4x)
=-4x2+60x+400
=-4(x-
| 15 |
| 2 |
∴当x=
| 15 |
| 2 |

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
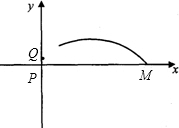





 的表达式、隧道的跨度AB和拱高OC.
的表达式、隧道的跨度AB和拱高OC.