题目内容
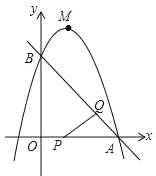
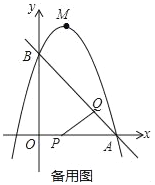
【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(m,n)(m<0,
n>0),E点在边BC上,F点在边OA上.将矩形OABC沿EF折叠,点B正好与点O重合,双曲线![]() 过点E.
过点E.
(1) 若m=-8,n =4,直接写出E、F的坐标;
(2) 若直线EF的解析式为![]() ,求k的值;
,求k的值;
(3) 若双曲线![]() 过EF的中点,直接写出tan∠EFO的值.
过EF的中点,直接写出tan∠EFO的值.

【答案】(1)E(-3,4)、F(-5,0);(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1) 连接OE,BF,根据题意可知:![]() 设
设![]() 则
则![]() 根据勾股定理可得:
根据勾股定理可得:![]() 即
即![]() 解得:
解得:![]() 即可求出点E的坐标,同理求出点F的坐标.
即可求出点E的坐标,同理求出点F的坐标.
(2) 连接BF、OE,连接BO交EF于G由翻折可知:GO=GB,BE=OE,证明△BGE≌△OGF,证明四边形OEBF为菱形,令y=0,则![]() ,解得
,解得![]() , 根据菱形的性质得OF=OE=BE=BF=
, 根据菱形的性质得OF=OE=BE=BF=![]() 令y=n,则
令y=n,则![]() ,解得
,解得![]() 则CE=
则CE=![]() ,在Rt△COE中, 根据勾股定理列出方程
,在Rt△COE中, 根据勾股定理列出方程![]() ,即可求出点E的坐标,即可求出k的值;
,即可求出点E的坐标,即可求出k的值;
(3) 设EB=EO=x,则CE=-m-x,在Rt△COE中,根据勾股定理得到(-m-x)2+n2=x2,解得![]() ,求出点E(
,求出点E(![]() )、F(
)、F(![]() ),根据中点公式得到EF的中点为(
),根据中点公式得到EF的中点为(![]() ),将E(
),将E(![]() )、(
)、(![]() )代入
)代入![]() 中,得
中,得![]() ,得m2=2n2
,得m2=2n2
即可求出tan∠EFO=![]() .
.
解:(1)如图:连接OE,BF,

E(-3,4)、F(-5,0)
(2) 连接BF、OE,连接BO交EF于G由翻折可知:GO=GB,BE=OE

可证:△BGE≌△OGF(ASA)
∴BE=OF
∴四边形OEBF为菱形
令y=0,则![]() ,解得
,解得![]() ,∴OF=OE=BE=BF=
,∴OF=OE=BE=BF=![]()
令y=n,则![]() ,解得
,解得![]() ∴CE=
∴CE=![]()
在Rt△COE中,![]() ,
,
解得![]()
∴E(![]() )
)
∴![]()
(3) 设EB=EO=x,则CE=-m-x,
在Rt△COE中,(-m-x)2+n2=x2,解得![]()
∴E(![]() )、F(
)、F(![]() )
)
∴EF的中点为(![]() )
)
将E(![]() )、(
)、(![]() )代入
)代入![]() 中,得
中,得
![]() ,得m2=2n2
,得m2=2n2
∴tan∠EFO=![]()

【题目】现有A、B两种手机上网计费方式,收费标准如下表所示:
计费方式 | 月使用费/元 | 包月上网时间/分 | 超时费/(元/分) |
A | 30 | 120 | 0.20 |
B | 60 | 320 | 0.25 |
设上网时间为x分钟,
(1)若按方式A和方式B的收费金额相等,求x的值;
(2)若上网时间x超过320分钟,选择哪一种方式更省钱?