Question

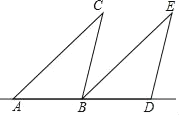
【题目】如图，已知：AD为△ABC的中线，过B、C两点分别作AD所在直线的垂线段BE和CF，E、F为垂足，过点E作EG∥AB交BC于点H，连结HF并延长交AB于点P。

（1）求证：DE=DF

（2）若；①求：的值；②求证：四边形HGAP为平行四边形。

Answer 1

【答案】（1）见解析；（2）①，②见解析.

【解析】

（1）根据AD是△ABC的中线得到BD＝CD，根据对顶角相等得到∠FDC＝∠EDB，又因为∠DFC＝∠DEB＝90°，即可证得△BDE≌△CDF，继而证出DE=DF；（2）设BH＝11x，HC＝5x，则BD＝CD＝BC＝8x，DH＝3x，HC＝5x，根据EH∥AB可得△EDH∽△ADB，再根据相似三角形对应边成比例以及DE＝DF得到的值；②进一步求出的值，得到，再根据平行线分线段成比例定理证得FH∥AC ，即PH∥AC，再根据两组对边分别平行的四边形是平行四边形这一定理即可证得四边形HGAP为平行四边形。

解：（1）∵AD是△ABC的中线，∴BD＝CD，

∵∠FDC和∠EDB是对顶角，∴∠FDC＝∠EDB ，

又∵BE⊥AE，CF⊥AE，∴∠DFC＝∠DEB＝90°，

∴△BDE≌△CDF（AAS），∴DE=DF.

（2）设则

① ∵EH∥AB

∴△EDH∽△ADB ∴∵

∴

②∵ ∴∵∴FH∥AC ∴PH∥AC

∵EG∥AB∴四边形HGAP为平行四边形