题目内容
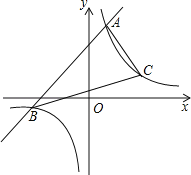
【题目】如图,一次函数y=![]() x-1的图象与坐标轴分别交于A、B两点,与反比例函数y=
x-1的图象与坐标轴分别交于A、B两点,与反比例函数y=![]() 的图象在第二象限的交点为点C,CD⊥x轴,垂足为点D,若C点横坐标为-4,
的图象在第二象限的交点为点C,CD⊥x轴,垂足为点D,若C点横坐标为-4,
(1)反比例函数的关系式及E点坐标;
(2)利用图像,当x<0时,写出![]()
![]() 的解集.
的解集.
【答案】(1)![]() ,E(2,
,E(2,![]() );(2)
);(2)![]() <
<![]()
【解析】
(1)由一次函数与坐标轴的交点求出OA,OB的长,证明△CBD≌△ABO,求出CD=OA,得到C点坐标,从而确定反比例函数关系式,再联立方程组,从而可求出E点坐标;
(2)根据函数图象可以确定不等式![]()
![]() 的解集.
的解集.
(1)在一次函数y=![]() x-1中,令x=0,则y=-1;令y=0,则x=-2.
x-1中,令x=0,则y=-1;令y=0,则x=-2.
∴OA=1,OB=2,
∵C点横坐标为-4,
∴OD=4,
∴DB=DO-BO=4-2=2,
∴OB=DB,
∵CD⊥x轴,
∴∠CDB=∠AOB
又∠CBD=∠ABO
∴△CDB≌△ABO
∴CD=OB=1
∴C(-4,1),
把C(-4,1)代入![]() 得,k=-4,
得,k=-4,
∴![]()
联立方程组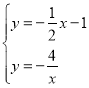 ,解得
,解得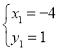 ,
,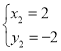
∴E(2,-2);
(2)根据图象可以得出,当![]() <
<![]() 时,
时,![]()
![]() .
.
所以,不等式![]()
![]() 的解集为x<-4.
的解集为x<-4.

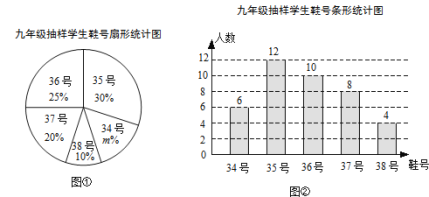
 全能测控期末小状元系列答案
全能测控期末小状元系列答案【题目】小华同学经过调查,了解到某客车租赁公司有![]() ,
,![]() 两种型号的客车,并得到了下表中的信息.
两种型号的客车,并得到了下表中的信息.
车型 |
|
|
|
| |
座位 | 45座 | 60座 |
信息 | 每辆 | |
5辆 | ||
(1)求每辆![]() 型和
型和![]() 型客车每天的租金各是多少元?
型客车每天的租金各是多少元?
(2)小华所在学校准备组织七年级全体学生外出一天进行研学活动,小华同学设计了下面甲乙两种租车方案:
方案甲:只租用![]() 型客车,但有一辆客车会空出30个座位.
型客车,但有一辆客车会空出30个座位.
方案乙:只租用![]() 型客车,刚好坐满,且比方案甲少用两辆客车.
型客车,刚好坐满,且比方案甲少用两辆客车.
求小华所在学校七年级学生的总人数.
(3)如果从节省费用的角度考虑,是否还有其他租车方案?如果有,请直接写出一种租车方案;如果没有,请说明理由。