��Ŀ����
����Ŀ����ѧʵ���ң�

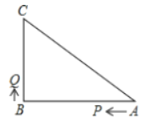
����4��ȫ�ȵ�ֱ��������ֽƬ����ͼ1��������4��ֽƬƴ�����ҳ�cΪ�߳��������ι�������ͼ������ͼ2�����Ŵ���ѧ����������ͼ����֤�˹��ɶ�����
̽���о���
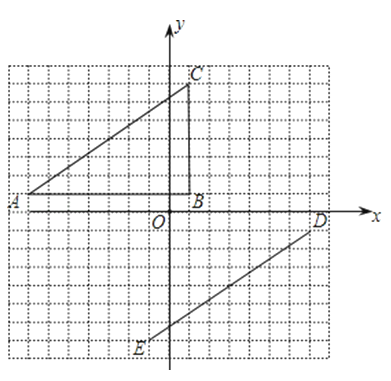
��1��С��������ͼ���е�2�������ν������˶��任���õ�ͼ3��������ͼ3֤�����ɶ�����
��ѧ˼����
��2��С����Ϊ�������ķ����ı�����ͼ����ijЩ�����ε�λ�ã�Ҳ����֤�����ɶ�����������һ�ַ���֧�����Ĺ۵㣨���ڱ���ͼ�в�ȫͼ�Σ�������֤������
���𰸡���1��֤������������2��֤����������
��������
��1��ͨ��ͼ�ε���������ּ��㷽�������ɵó������
��2��ͨ������������������ּ��㷽�������ɵó������
��1���⣺��ͼ3��ʾ��
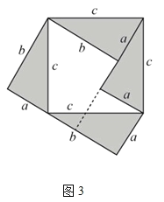
ͼ�ε������ʾΪ��![]() ��
��
ͼ�ε����Ҳ�ɱ�ʾ��![]() ��
��
��a2b2abc2ab��
��a2b2c2
��2���⣺��ͼ4��ʾ��
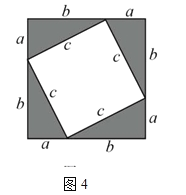
�������ε������ʾΪ��ab2��
�������ε����Ҳ���Ա�ʾΪ��![]() ��
��
��![]() ��
��
��a2b22abc22ab��
��a2b2c2��

����Ŀ��ij��Ϊ�˾������ƶ��������״��������Ӧ���Һ��٣�15λ������8��Ԫ���а���һЩ������ֲ�л��߲˺�ˮ����������������ÿ������Ҫ������Ͷ���ʽ����±���
�������� | ÿ������������/�� | ÿ����Ͷ���ʽ�/��Ԫ |
�߲� | 4 | 2 |
ˮ�� | 5 | 3 |
�����������£���15λ����Ӧ�а����ٹ������أ�����������ʹÿ�˶����¿����������ʽ����ù��ã�