Question

【题目】乘法公式的探究与应用：

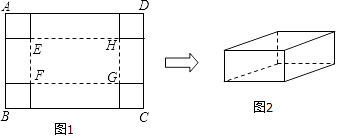
（1）如图甲，边长为a的大正方形中有一个边长为b的小正方形，请你写出阴影部分的面积是　 　

（2）小颗将阴影部分接下来，重新拼成一个长方形，如图乙，则长方形的长是　 　，宽是　 　，面积是　 　（写成多项式乘法的形式）．

（3）比较甲乙两图阴影部分的面积，可以得到恒等式　 　

（4）运用你所得到的公式计算：10.3×9.7．

（5）若49x2﹣y2＝25，7x﹣y＝5，则7x+y的值为　 　

Answer 1

【答案】（1）a2﹣b2；（2）a+b，a﹣b，（a+b）（a﹣b）；（3）（a+b）（a﹣b）=a2﹣b2；（4）99.91；（5）5

【解析】

（1）由图形可知长和宽的值，再根据正方形面积公式可得答案；

（2）由图形可知长方形的长和宽，根据长方形面积公式可得答案；

（3）由（1）（2）结论直接得答案；

（4）应用（3）的公式可简算，从而得答案；

（5）先将49x2-y2=25左边用平方差公式展开，再将7x-y=5代入可得答案．

解：（1）阴影部分的面积＝大正方形的面积﹣小正方形的面积＝a2﹣b2

故答案为：a2﹣b2．

（2）长方形的长是（a+b），宽是（a﹣b），面积＝长×宽＝（a+b）（a﹣b）

故答案为：a+b；a﹣b；（a+b）（a﹣b）．

（3）由（1）（2）可得（a+b）（a﹣b）＝a2﹣b2

故答案为：（a+b）（a﹣b）＝a2﹣b2．

（4）10.3×9.7

＝（10+0.3）（10﹣0.3）

＝102﹣0.32

＝100﹣0.09

＝99.91

（5）∵49x2﹣y2＝25，

∴（7x+y）（7x﹣y）＝25

∵7x﹣y＝5

∴（7x+y）×5＝25

∴7x+y＝5

故答案为：5．