题目内容
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,如图1,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面为矩形EFGH,如图2.设小正方形的边长为x厘米.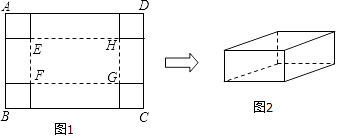
(1)当矩形纸板ABCD的一边长为90厘米时,求纸盒的侧面积的最大值;
(2)当EH:EF=7:2,且侧面积与底面积之比为9:7时,求x的值.
【答案】
(1)解:∵矩形纸板ABCD的一边长为90cm,
∴矩形纸板的另一边长为3600÷90=40(cm),
则S侧=2[x(90﹣2x)+x(40﹣2x)]=﹣8x2+260x,
=﹣8(x﹣ ![]() )2+
)2+ ![]() .
.
∵﹣8<0,
∴当x= ![]() 时,S侧最大=
时,S侧最大= ![]()
(2)解:设EF=2m,则EH=7m,
则侧面积为2(7mx+2mx)=18mx,底面积为7m2m=14m2,
由题意,得18mx:14m2=9:7,
∴m=x.
则AD=7x+2x=9x,AB=2x+2x=4x
由4x9x=3600,且x>0,
∴x=10
【解析】(1)最值问题可运用函数思想解决,设出自变量x,函数为纸盒的侧面积y,构建二次函数,配成顶点式,求出最大值;(2)用x的代数式表示出侧面积与底面积,根据9:7,再根据总面积为3600,建立方程,求出x.

练习册系列答案
相关题目