Question

【题目】（10分）已知⊙O为△ABC的外接圆，圆心O在AB上．

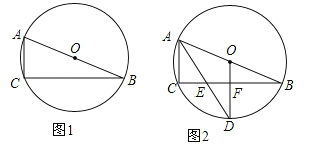
（1）在图1中，用尺规作图作∠BAC的平分线AD交⊙O于D（保留作图痕迹，不写作法与证明）；

（2）如图2，设∠BAC的平分线AD交BC于E，⊙O半径为5，AC=4，连接OD交BC于F．

①求证：OD⊥BC；

②求EF的长．

Answer 1

【答案】（1）作图见试题解析；（2）①证明见试题解析；②．

【解析】

试题分析：（1）按照作角平分线的方法作出即可；

（2）①由AD是∠BAC的平分线，得到，再由垂径定理推论可得到结论；

②由勾股定理求得CF的长，然后根据平行线分线段成比例定理求得，即可求得，继而求得EF的长．

试题解析：（1）尺规作图如图1所示：

（2）①如图2，∵AD平分∠BAC，∴∠DAC=∠BAD，∴， ∵OD过圆心，∴OD⊥CB；

②∵AB为直径，∴∠C=90°，∵OD⊥CB，∴∠OFB=90°，∴AC∥OD，∴，，即，∴OF=2，∵FD=5﹣2=3，在RT△OFB中，BF===，∵OD⊥BC，∴CF=BF=，∵AC∥OD，∴△EFD∽△ECA，∴，∴，∴EF=CF==．