题目内容
【题目】如图,在边长为2的等边△ABC中,AD⊥BC,点P为边AB 上一个动点,过点P作PF∥AC交线段BD于点F,作PG⊥AB交AD于点E,交线段CD于点G,设![]() ,
, ![]() .
.
(1)求证: ![]() ;
;
(2)求y关于x的函数解析式,并写出x的取值范围;
(3)以P、E、F为顶点的三角形与△EDG能否相似?如果能相似,请求出.BP的长,如果不能,请说明理由.

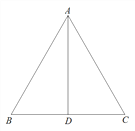
(备用图)
【答案】(1);(2)![]() (
(![]() ≤
≤![]() ≤1);(3)
≤1);(3)![]() 或
或![]() .
.
【解析】试题分析:(1)证△PBF是等边三角形,得到BF=FP.再由等角对等边得到FP=FG,从而得到结论;
(2)由BP=x,∠PGB=30°,得到![]() ,
, ![]() .由等边三角形的性质得到BD=1,
.由等边三角形的性质得到BD=1,
从而有DG=2x-1,在△EDG中,得到DG=![]() y,故2x-1=
y,故2x-1=![]() y,从而得到结论.
y,从而得到结论.
(3)若△FPE与△EDG相似,分两种情况讨论:①当![]() 时;②当
时;②当![]() 时.
时.
试题解析:解:(1)∵△ABC为等边三角形,∴![]()
又∵PF∥AC,∴![]() ,∴△PBF是等边三角形,∴
,∴△PBF是等边三角形,∴ ![]() .
.
又∵PG⊥AB,∴![]() ,∴
,∴ ![]() ,∴
,∴ ![]() .
.
(2)∵![]() ,
, ![]() ,
, ![]() ,∴
,∴ ![]() ,
, ![]() .
.
又∵△ABC是等边三角形,AD⊥BC, ![]() ,∴
,∴ ![]() ,∴
,∴ ![]()
在△EDG中,∵∠EDG=90°,∠EGD=30°,ED=y,∴DG=![]() y,
y,
∴2x-1=![]() y,∴
y,∴ ![]() (
(![]() ≤
≤![]() ≤1).
≤1).
(3)能相似,
∵![]() ,∴若△FPE与△EDG相似,有两种情况.
,∴若△FPE与△EDG相似,有两种情况.
①当![]() 时,∴EF∥AB,∴
时,∴EF∥AB,∴![]() ,∴
,∴![]() ,解得:
,解得: ![]() ;
;
②当![]() 时,
时,
∵△BPF是等边三角形,∴![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,
,
∵AD⊥BC,∴![]() , 即
, 即![]() ,解得:
,解得: ![]() , ∴BP的长是
, ∴BP的长是![]() 或
或![]()

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
