Question

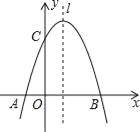
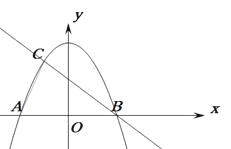
【题目】如图，抛物线与x轴交于A，B两点，与直线相交于B，C两点，连结A，C两点。

（1）写出直线BC的解析式

（2）求△ABC的面积

Answer 1

【答案】（1）y=-x+；（2）．

【解析】

试题（1）利用抛物线，令y=0，解方程求出点A、B的坐标，然后把点B的坐标代入直线BC的解析式求出b的值，即可得解；

（2）根据点A、B的坐标求出AB的长度，再把抛物线解析式与直线BC的解析式联立求解得到点C的坐标，然后根据三角形的面积公式列式计算即可得解；

试题解析：（1）令y=0，则﹣x2+3=0，

解得x1=﹣2，x2=2，

所以，点A（﹣2，0），B（2，0），

所以，﹣×2+b=0，

解得b=，

所以，直线BC的解析式为y=﹣x+；

（2）∵点A（﹣2，0），B（2，0），

∴AB=2﹣（﹣2）=2+2=4，

联立，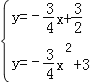

解得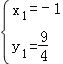，（为点B坐标，舍去），

所以，点C的坐标为（﹣1，），

所以，△ABC的面积=×4×=；