题目内容
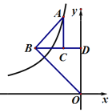
【题目】已知⊙O的弦CD与直径AB垂直于F,点E在CD上,且AE=CE.

(1)求证:CA2=CE CD;
(2)已知CA=5,EC=3,求sin∠EAF.
【答案】(1)证明见解析;(2)sin∠EAF=![]() .
.
【解析】试题分析:
(1)由已知条件易得∠CAE=∠D,结合∠C是公共角可得△CEA∽△CAD,从而可得:![]() ,由此即可得到:CA2=CE ·CD;
,由此即可得到:CA2=CE ·CD;
(2)由CA2=CE ·CD结合CA=5,EC=3,可求出CD的长,结合F是CD的中点可求得CF的长,从而由EF=CF-EC求得EF的长,这样结合AE=EC=3在Rt△AEF中即可求得sin∠EAF的值了.
试题解析:
(1)∵弦CD⊥直径AB,
∴![]() ,
,
∴∠D=∠C,
又∵AE=EC,
∴∠CAE=∠C,
∴∠CAE=∠D,
∵∠C是公共角,
∴△CEA∽△CAD,
∴![]() ,
,
∴CA2=CE![]() CD;
CD;
(2)∵CA2=CE![]() CD,AC=5,EC=3,
CD,AC=5,EC=3,
∴52=CD![]() 3,
3,
解得:CD=![]() ,
,
又∵CF=FD,
∴CF=![]() CD=
CD=![]() ×
×![]() =
=![]() ,
,
∴EF=CF-CE=![]() -3=
-3=![]() ,
,
在Rt△AFE中,sin∠EAF=![]() .
.

练习册系列答案
相关题目