题目内容
【题目】在平面直角坐标系xOy中,对于与坐标轴不平行的直线l和点P,给出如下定义:过点P作x轴,y轴的垂线,分别交直线l于点M,N,若PM+PN≤4,则称P为直线l的近距点,特别地,直线上l所有的点都是直线l的近距点.已知点A(-![]() ,0),B(0,2),C(-2,2).
,0),B(0,2),C(-2,2).
(1)当直线l的表达式为y=x时,
①在点A,B,C中,直线l的近距点是 ;
②若以OA为边的矩形OAEF上所有的点都是直线l的近距点,求点E的纵坐标n的取值范围;
(2)当直线l的表达式为y=kx时,若点C是直线l的近距点,直接写出k的取值范围.

【答案】(1)①A,B;②n的取值范围是![]() ,且
,且![]() ;(2)
;(2) ![]() .
.
【解析】(1)①根据PM+PN≤4,进行判断;②当PM+PN=4时,可知点P在直线l1:![]() ,直线l2:
,直线l2:![]() 上.所以直线l的近距点为在这两条平行线上和在这两条平行线间的所有点.分两种情况EF在OA上方,当点E在直线l1上时,n的值最大;EF在OA下方,当点F在直线l2上时,n的值最小,当
上.所以直线l的近距点为在这两条平行线上和在这两条平行线间的所有点.分两种情况EF在OA上方,当点E在直线l1上时,n的值最大;EF在OA下方,当点F在直线l2上时,n的值最小,当![]() 时,EF与AO重合,矩形不存在,所以可以分析出n的取值范围;
时,EF与AO重合,矩形不存在,所以可以分析出n的取值范围;
(2)根据定义,结合图形可推出:![]() .
.
解:(1)①A,B;
②当PM+PN=4时,可知点P在直线l1:![]() ,直线l2:
,直线l2:![]() 上.所以直线l的近距点为在这两条平行线上和在这两条平行线间的所有点.
上.所以直线l的近距点为在这两条平行线上和在这两条平行线间的所有点.
如图1,EF在OA上方,当点E在直线l1上时,n的值最大,为![]() .
.
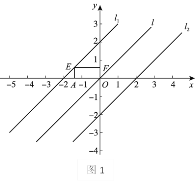
如图2,EF在OA下方,当点F在直线l2上时,n的值最小,为![]() .
.

当![]() 时,EF与AO重合,矩形不存在.
时,EF与AO重合,矩形不存在.
综上所述,n的取值范围是![]() ,且
,且![]() .
.
(2)![]() .
.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案【题目】甲、乙两人5次射击命中的环数如下:
甲 | 7 | 9 | 8 | 6 | 10 |
乙 | 7 | 8 | 9 | 8 | 8 |
则以下判断中正确的是( )
A.![]() 甲=
甲= ![]() 乙 , S甲2=S乙2 .
乙 , S甲2=S乙2 .
B.![]() 甲=
甲= ![]() 乙 , S甲2>S乙2 .
乙 , S甲2>S乙2 .
C.![]() 甲=
甲= ![]() 乙 , S甲2<S乙2 .
乙 , S甲2<S乙2 .
D.![]() 甲<
甲< ![]() 乙 , S甲2<S乙2 .
乙 , S甲2<S乙2 .