��Ŀ����
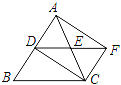
����Ŀ��С����ѧϰ������֪ʶʱ����������������Ȥ�Ľ��ۣ���Rt��ABC�У���A��90�㣬BDƽ�֡�ABC��MΪֱ��AC��һ�㣬ME��BC������ΪE����AME��ƽ���߽�ֱ��AB�ڵ�F��
��1����ͼ�٣�MΪ��AC��һ�㣬��BD��MF��λ�ù�ϵ�� ��
��ͼ�ڣ�MΪ��AC�����ӳ�����һ�㣬��BD��MF��λ�ù�ϵ�� ��
��ͼ�ۣ�MΪ��AC�ӳ�����һ�㣬��BD��MF��λ�ù�ϵ�� ��
��2�����ͼ�١�ͼ�ڡ���ͼ���е�һ�����������֤��.

���𰸡���1��BD��MF��BD��MF��BD��MF����2��֤����������
��������
���⣨1��ƽ�У���ֱ����ֱ�� 3��
��2��ѡ�� ֤��BD��MF
�������£��ߡ�A=90����ME��BC��
���ABC+��AME=360�㩁90���2=180���� 1��
��BDƽ����ABC��MFƽ����AME��
���ABD=![]() ��ABC����AMF=
��ABC����AMF=![]() ��AME��
��AME��
���ABD+��AMF=![]() ����ABC+��AME��=90���� 2��
����ABC+��AME��=90���� 2��
���ߡ�AFM+��AMF=90����
���ABD=��AFM�� 3��
��BD��MF�� 4��
ѡ�� ֤��BD��MF��
�������£��ߡ�A=90����ME��BC��
���ABC+��C=��AME+��C=90����
���ABC=��AME�� 1��
��BDƽ����ABC��MFƽ����AME��
���ABD=��AMF�� 2��
�ߡ�ABD+��ADB=90����
���AMF+��ADB=90���� 3��
��BD��MF�� 4��
ѡ�� ֤��BD��MF��
�������£��ߡ�A=90����ME��BC��
���ABC+��ACB=��AME+��ACB=90����
���ABC=��AME�� 1��
��BDƽ����ABC��MFƽ����AME��
���ABD=��AMF�� 2��
�ߡ�AMF+��F=90����
���ABD+��F=90���� 3��
��BD��MF�� 4��