题目内容
【题目】如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B与点D重合,折痕分别交边AB、BC于点F、E,若AD=2,BC=8.
(1)求BE的长;
(2)求∠CDE的正切值.

【答案】(1)5;(2)![]() .
.
【解析】
试题
(1)由折叠的性质易证BE=DE,由此可得∠BDE=∠DBE=45°,从而得到∠DEB=90°,说明DE是等腰梯形的高,由此可得EC=![]() (BC﹣AD)=3;
(BC﹣AD)=3;
(2)由(1)可得∠DE90°,EC=3,DE=BE=BC-EC=5,从而可得tan∠CDE=![]() .
.
试题解析:
(1)∵△DFE是△BFE翻折而成,
∴△BFE≌△DFE,
∴DE=BE,
∵∠DBE=45°,
∴∠BDE=∠DBE=45°,
∴△DBE中,∠DEB=90度.
∴DE⊥BC,即DE是等腰梯形ABCD的高,
又∵在等腰梯形ABCD中,AD∥BC,AD=2,BC=8,
∴EC=![]() (BC﹣AD)=3.
(BC﹣AD)=3.
∴BE=BC﹣EC=5;
(2)由(1)可得,∠DEC=90°,DE=BE=5.
∵在△DEC中,∠DEC=90°,DE=5,EC=3,
∴tan∠CDE=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
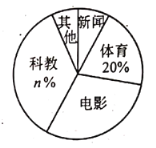
【题目】学校为了解全校![]() 名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
频道 | 新闻 | 体育 | 电影 | 科教 | 其他 |
人数 |
|
|
|
|
|
![]() 求调查的学生人数及统计图表中
求调查的学生人数及统计图表中![]() 的值;
的值;
![]() 求选择其他频道在统计图中对应扇形的圆心角的度数;
求选择其他频道在统计图中对应扇形的圆心角的度数;
![]() 求全校最爱选择电影频道的学生人数.
求全校最爱选择电影频道的学生人数.